A Look at Brahmagupta's Formula

by Amy Benson

We begin this investigation by recalling Heron's formula for finding the area of a triangle:

where s is the semiperimeter of the triangle and a, b, and c are the lengths of the sides of the triangle as shown.

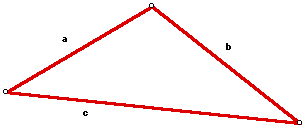
Can Heron's formula be applied more generally to a quadrilateral so that

where s is the semiperimeter of the quadrilateral? We know that if d = 0, then the formula is indeed correct. Alas, this conjecture is not always true. The conjecture is true in the instance when the quadrilateral is inscribed in a circle and this is Brahmagupta's formula.

So, let us examine the situation visually.

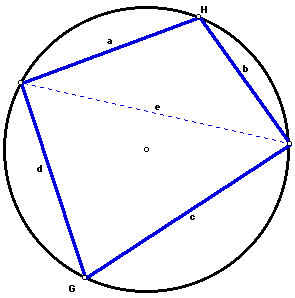
First we insert the diagonal e of the quadrilateral. We know that m<G + m<H = 180 degrees because they are inscribed angles that intercept a major and minor arc that together measure 360 degrees. From this, we know that cos G = - cos H and sin G = sin H. Using the law of cosines,

and that

so

Substituting cosH for - cos G,

and this leads to

so (*)

The area A of a quadrilateral is given by

or simplified

Then (**)

Taking the two starred equations, adding and squaring them, we see that

At this point, we will focus on factoring the left side of this equation using

So,

Finally, let x = a+b and y = c- d. So,

Recall that s = 0.5 (a + b + c + d), so 2s = a + b + c + d.

Then,

or

Therefore,

proving Brahmagupta's formula for the area of a quadrilateral inscribed in a circle.

Reference: Precalculus Mathematics in a Nutshell: Geometry, Algebra, Trignometry by George F. Simmons. Jansen Publications, Inc. 1987.

Return to Amy Benson's Homepage