

Problem: Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extented to their intersections with the opposite sides in points D, E, and F respectively.
First we need to illustrate the question at hand.
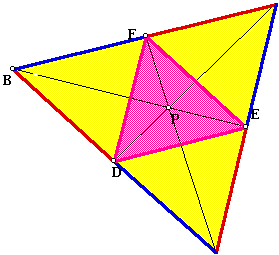
Let us examine the ratio of (AF)(BD)(EC) to (FB)(CD)(AE). For all positions of P in the interior of triangle ABC, this ratio is 1. Notice also that that by breaking this ratio into smaller components [ratio of AF to FB, ratio of EC to AE, and ratio of BD to CD], we find that the product of any pair of these ratios is the multiplicative inverse of the third ratio. This offers some explanation of the first ratio being 1. To explore this yourself, click here.
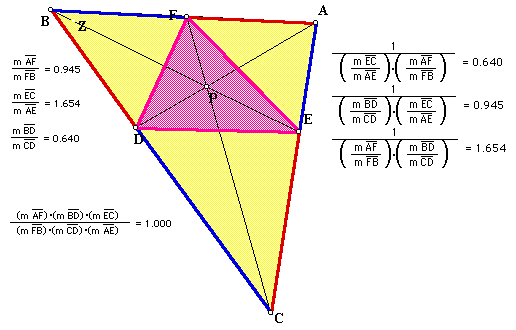
To investigate this ratio more thoroughly and see some proof, click here.
It is also valuable to ensure our findings hold if P is located outside of triangle ABC.
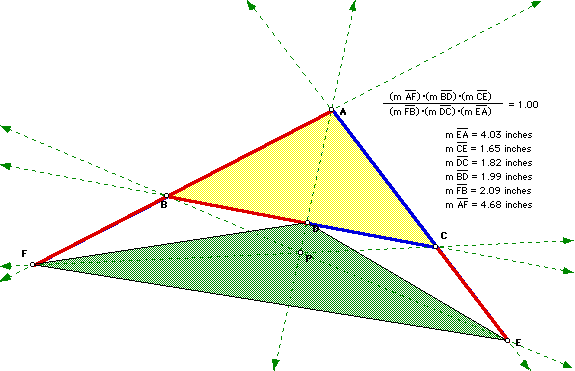
The illustration indicates that it does. Click here to explore more in depth.
Also of interest is the ratio of the area of triangle ABC to the area of triangle FED. This ratio is always greater than or equal to 4 when point P is inside triangle ABC. The ratio is 4 when point P is the centroid of triangle ABC. This fact may be confirmed in several ways. Moving point P to a position such that the ratio is 4, confirm that AP is two-thirds of AD, CP is two-thirds of CF, and BP is two-thirds of BE. Also, see that F, D, and E are the midpoints of segments AB, BC, and AC, respectively. To check the assertion that the ratio is 4, find the areas of BED, FED, AEF, and CED. They should be equal, each one fourth of the area of ABC.
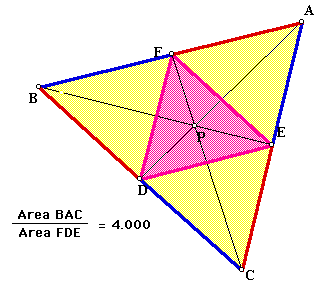
Click here to investigate further.