Constructing a Circle Tangent to a Given Line

and a Given Circle

by Amy Benson

We begin with a given circle and a given line, such as

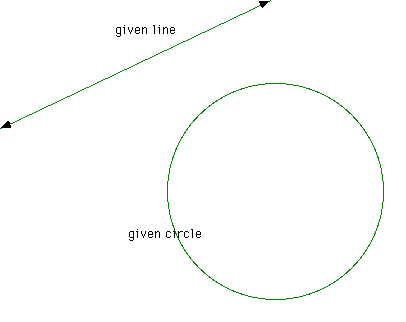
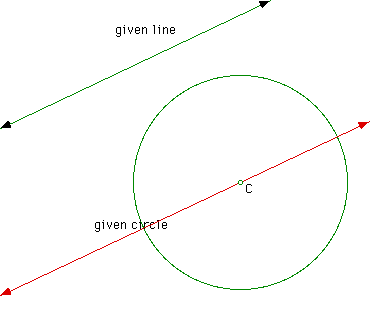
The task at hand in to construct a circle that is tangent to both of the givens at the same time. First, construct a line parallel to the given line through the center of the given circle.

Next, construct a line perpendicular to these two lines through the center of the circle.

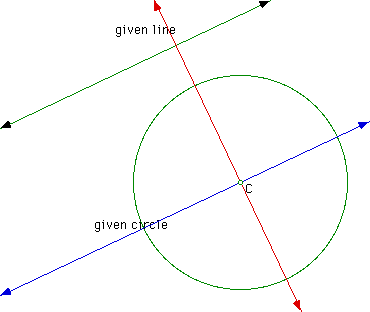
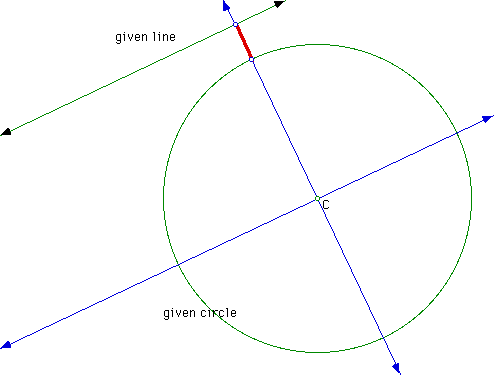
Construct a point of intersection between the perpendicular and the given circle as well as the point of intersection between the perpendicular and the given line.

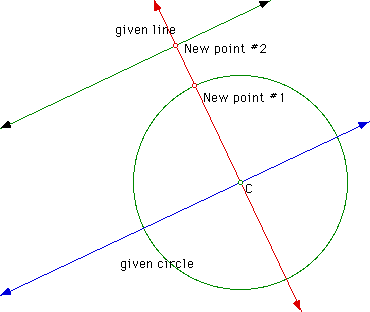
Construct a segment between these two points of intersection.

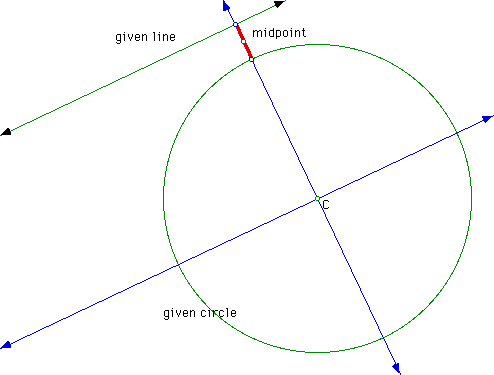
Construct the midpoint of this segment (this is the center of the tangent circle).

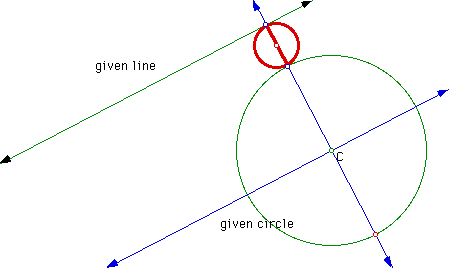
Construct the circle with this center and a point on the circle being one of the points of intersection.

To see the effects of changing one or both of the givens and to confirm that the constructed (red) circle does indeed remain tangent to both the given line and the given circle at all times, click here. To use a script of this construction with your own given circle and line, click here.

Return to Amy Benson's Homepage