

Every time hit a trig button on my calculator, the calculator "knows" the answer and responds appropriately. As I am constantly encouraging my students not to rely on their calculators for everything (after all a machine is only as good as its operator), I want to find the values of the sine, cosine, and tangent of 5 degrees through 90 degrees in increments of 5 degrees.
I begin with the basic right isosceles triangle
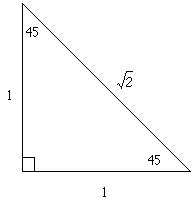
Recall that
So,
If I am to compare these values to the values I obtain from my calculator, I must approximate:
Now, I shift my focus to an equilateral triangle with sides of length 1 unit. I will use this triangle to find the values of the trigonometric ratios for 30 degrees and 60 degrees.
Using the Pythagorean Theorem, I find that the perpendicular
bisector (height of the triangle) of one side of the triangle
is ![]() .
.
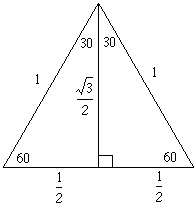
So,
while
Again, approximation is required:
At this point, in my computations, I need a few helpful formulas:
With these formulas, I will find compute the sine, cosine and
tangent of ![]() ,
, ![]() , and
, and ![]() .
.
Starting with ![]() , I use the half-angle formula
to find the cosine.
, I use the half-angle formula
to find the cosine.
Having found the cosine, I easily find the sine.
Now, the tangent:
In order to find the values of the trigonometric functions
for ![]() , I use the values I found when x=
, I use the values I found when x=![]() and
and
x=![]() .
.
This leads to
and
Next, I look at x=![]() .
.
and
and
To go any further, I will ahve to use the sine power series. I begin this portion of my computations I use
To compute sin ![]() , I use a TI-82 graphing calculator.
First, I convert
, I use a TI-82 graphing calculator.
First, I convert ![]() to
to ![]() and
store this value as x. Then, I program the calculator to sum the
series accurate to nine decimal places. The steps are as follows:
and
store this value as x. Then, I program the calculator to sum the
series accurate to nine decimal places. The steps are as follows:
yields
So, I know continue my computations confident that the ![]() .
.
I use my newly found value to find the value of cosine:
and the tangent value:
All subsequent computations to find the values of the three trignometric functions in question involve the use of aforementioned trignometric formulas. Hence, if you wish to see those computations, click here. Otherwise, here is the table of values:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In order to complete a similar table with angles by increments
of ![]() instead of
instead of ![]() , use the sine/cosine
power series to find the trignometric values at
, use the sine/cosine
power series to find the trignometric values at ![]() and
then systematically use the formulas used in this essay to find
all subsequent values.
and
then systematically use the formulas used in this essay to find
all subsequent values.
Return to Amy Benson's Homepage