Assignment 1 Write-Up
The Problem:
Examine graphs of y = a sin(bx + c) for different values of a, b, and c.
The Strategy:
For this problem, we will begin by trying different values for "a", then for "b", and finally for "c". After seeing how each variable interacts individually, we will begin to change the variables together, seeing if the variables have any interaction that may produce interesting results.
Foundation:
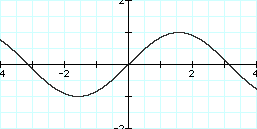
Well, let's see what the graph of y = sin x looks like....
Graph: y = sin x

That's nothing we haven't seen before. For reference, we'll keep this graph on the screen each time something is changed. (It will always be in black or gray.)
Changing the Variable "a":
It's time to start playing with the variable "a". We're going to graph y = a sin x and see what happens when we change "a".
Graph: y = 2 sin x and y = sin x
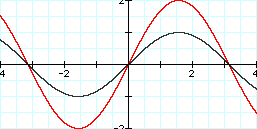
This is interesting. Notice how multiplying by 2 stretched the graph vertically. However, it did not change any of the x-intercepts. I would surmise (based on my knowledge from manipulating functions) that multiplying by 1/2 will shrink the graph vertically, while leaving the x-intercepts in the same place. Let's see....
Graph: y = 1/2 sin x and y = sin x
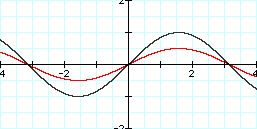
I was correct. Changing the "a" value to 1/2 shrunk the graph while leaving the x-intercepts alone. It is interesting to note that the maximum of the function is the "a" value. For example, the maximum of y = 1/2 sin x is 1/2. Similarly, the maximum of y = 2 sin x is 2. Also, the minimum of the function is simply the opposite of the "a" value or "-a". The minimum of y = 1/2 sin x is -1/2, and the minimum of y = 2 sin x is -2. The "a" value therefore determines the amplitude of the sine function. However, the "a" value does not always determine the maximum or minimum value of the sine function. If a "d" parameter is added-- y = d + a sin (bx + c) (we are not looking at a "d" parameter in this exploration), it would shift the graph vertically, which would also have an effect on the maximum and minimum of the function.
But what about negative values for "a"? Let's see what y = -3 sin x does....
Graph: y = -3 sin x and y = sin x
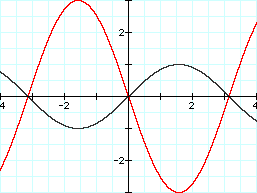
Wow! This changed things quite a bit. Like I thought, multiplying by -3 stretched the graph. However, the negative sign changed things a little. The graph is now reflected over the x-axis. Note, however, that the x-intercepts still have not changed. We'll do one more: y = -1/4 sin x
Graph: y = -1/4 sin x and y = sin x
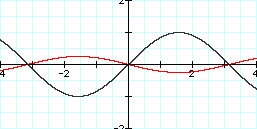
The same things happened here. The -1/4 shrunk the graph and flipped it over the x-axis: just like we expected. Let's move on to the "b" variable.
Changing the Variable "b":
Well, let's change the "b" variable. We'll start with something simple, like 2....
Graph: y = sin (2x) and y = sin x
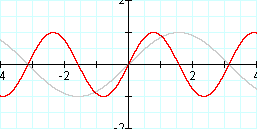
Like we would expect, this shrunk the graph horizontally. So if we were to make "b" 1/2, we would expect the graph to stretch horizontally, right? Let's see....
Graph: y = sin (1/2 x) and y = sin x
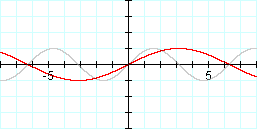
We were right. But what does the "b" variable specifically do? Since the sine function is a periodic function (or a repeating function), any horizontal stretch or shrink will affect the period of the function. Specifically, multiplying by 1/2 will double the period, and multiplying by 2 will half the period. Do you see the pattern? We know that the period of y = sin x is 2 PI. In general, the period is (1/b)*(2 PI). Therefore, the period of y = sin (1/2 x) is [1/(1/2)]*(2 PI) or 4 PI. In addition, the period of y = sin (2x) is (1/2)*(2 PI) or PI.
But what happens if the "b" variable is negative? We would surmise, based on our previous experience with the "a" variable, that making "b" negative would reflect the graph over the y-axis. Let's see....
Graph: y = sin (-x) and y = sin x
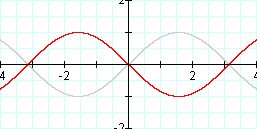
We were correct. There's something interesting to notice here. We mentioned before that the sine function is periodic. Reflecting the graph over the y-axis is the same as shifting it horizontally (in either direction) by 1/2 of its period, or in this case, PI. Remember this; it may come in handy later on.
Let's do a few more examples of manipulating the "b" variable, and then we'll move on to the "c" variable.
Graph: y = sin (-1/3 x) and y = sin x
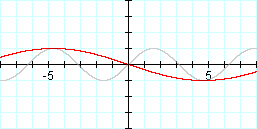
Like we would expect, the graph of y = sin (-1/3 x) results in a horizontal stretch and a reflection over the y-axis.
Graph: y = sin (-4x) and y = sin x
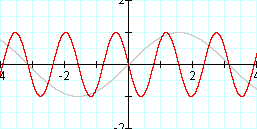
Once again, we have a reflection over the y-axis, but now also a horizontal shrink. What would the period of this function be, though? Remember the formula from above: (1/b)*(2 PI). Therefore the period of y = sin (-4x) is 1/2 PI. Note that the period is never negative, since a negative value for the period would result in the same positive value for the period. This shows that it doesn't matter which direction (left to right or right to left) you measure the period in.
Changing the Variable "c":
Once again, we'll start out with something simple. We'll try c = 1:
Graph: y = sin (x + 1) and y = sin x
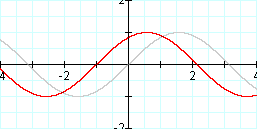
It looks like that resulted in a horizontal translation of 1 to the left. Let's try a negative value for "c". We would expect that this would result in a horizontal translation to the right. Let's see if we're right....
Graph: y = sin (x - 2) and y = sin x
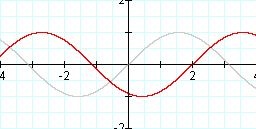
Like we expected, c = -2 results in a horizontal translation of 2 to the right. Remember that the sine function is periodic. Since it repeats, if we do a horizontal translation of the period (either to the left or the right), we should get the exact same graph. We know that the period of y = sin x is 2 PI. So let's try y = sin (x + (2 PI)).
Graph: y = sin (x + (2 PI)) and y = sin x
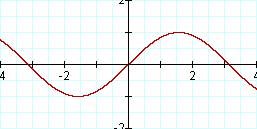
We got the same graph as y = sin x. This is very interesting. In general, any time you have a periodic function, a horizontal translation (in either direction) of the period will result in a graph that is exactly the same as the original.
Changing All of the Variables:
Now we are going to change all of the variables together. This isn't very tough. All we'll need to do is apply each of the stretches/shrinks, reflections, and translations.
Graph: y = 2 sin (2x + 2) and y = sin x
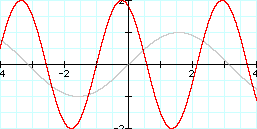
This is a vertical stretch of 2, a horizontal shrink by 1/2, and a horizontal translation of -2.
Graph: y = -1/2 sin (3x - 1) and y = sin x
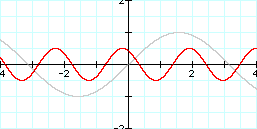
This is a vertical shrink of 1/2, a reflection over the x-axis, a horizontal shrink of 1/3, and a horizontal translation of 1.
Now we're going to try some interesting things which will result in a graph exactly the same as y = sin x.
Graph: y = - sin (-x) and y = sin x

This is very interesting. A reflection over the y-axis and a reflection over the x-axis results in the same graph.
Graph: y = sin (-x + PI) and y = sin x

Reflecting over the y-axis and then applying a horizontal translation of PI results in the same graph. This relates back to what we discussed earlier regarding reflections and period.
Graph: y = - sin (x + PI) and y = sin x

Reflecting over the x-axis and then applying a horizontal translation of PI also results in the same graph.
Conclusions:
Through this exploration we have seen how differing values of "a", "b", and "c" can affect the graph of the sine function. We have also seen how the variables interact, and how, in some ways, one variable can "undo" another. We touched on shrinks and stretchs, reflections, horizontal translations, and period. However, we failed to mention anything regarding vertical translations. It would be interesting to check on how a "d" variable ( y = d + a sin (bx+c) ) might affect the graph of the sine function. Also, what about composing the sine function: y = sin (sin (x)). Another thing that might be interesting to explore would be y = sin^2 (x).