Essay Number One
Circle Inversion
Introduction:
Circle Inversion is an operation in Euclidean Geometry, but inversion has connections to Hyperbolic Geometry as well. For our purposes, we will only look at the Euclidean operation of inversion in a circle.
Definition:
Call the circle of inversion circle I. Let the center of circle I be O. If P is the point to be inverted, then its image, P', satisfies the following: m(OP) * m(OP') = r2, where r is the radius of circle I. Note that if P=O, then P' does not exist. (It may help to think of P' as going to infinity in this case.)
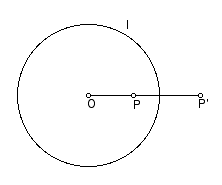
Consequences of the Definition:
The following properties of inversion are direct consequences of the definition.
- Every point on the circle of inversion is fixed. That is, if P lies on circle I, then P = P'. Similarly, if P = P', then P must lie on circle I. (Intuitive Proof: If P lies on circle I, then m(OP) is r. Thus, in order for the definition of inversion to be satisfied, m(OP') must be r as well. Therefore, P' must lie on circle I. If P = P', then the only way for the definition of inversion to be satisfied is for m(OP) = m(OP') = r, so P must lie on circle I.)
- If P is inside circle I, the P' is outside circle I. (Intuitive Proof: If P is inside circle I, then m(OP) < r. Thus, in order for the definition of inversion to be satisfied, m(OP') > r. Thus, P' is outside circle I.)
- If P is outside circle I, the P' is inside circle I. (Intuitive Proof: If P is outside circle I, then m(OP) > r. Thus, in order for the definition of inversion to be satisfied, m(OP') < r. Thus, P' is inside circle I.)
- (P')' = P (Intuitive Proof: Case (i)- P is inside circle I. Thus P' is outside circle I. Then (P')' must be inside circle I. Furthermore, in order for the definition of inversion to be satisfied, (P')' must equal P. Case (ii)- P is outside circle I. Proof for this case mimics Case (i).)
Seeing Inversion With GSP:
The following is a GSP sketch to help illustrate the definition of circle inversion. The radius and the lengths of important segments have been measured on this sketch to help us "see" the definition in action.
Inversion Sketch for GSP
Constructing Inverse Points:
Let's begin with two simple constructions of inverse points. We'll take two cases: P being inside circle I and P being outside circle I.
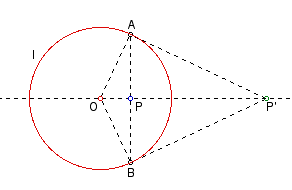
Simple Construction 1: P inside circle I
- Begin with a circle (circle I) and point P inside the circle.
- Construct a line between the center of circle I (point O) and P.
- Construct a line perpendicular to line OP through P.
- This line will intersect circle I at two points. Call these points A and B.
- Draw segments connecting O with A and O with B.
- Construct a line perpendicular to OA through A and a line perpendicular to OB through B.
- The intersection of these lines is your inverse point, P'.
- GSP Script for this Construction
Simple Construction 2: P outside circle I
- Begin with a circle (circle I) and point P inside the circle.
- Construct a segment between the center of circle I (point O) and P.
- Find the midpoint of this segment; label it M.
- Construct the circle with center M and radius MP.
- This circle will intersect circle I at two points. Call these points A and B.
- Draw a segment connecting A and B.
- Segement AB will intersect OP.
- The intersection of these segments is your inverse point, P'.
- GSP Script for this Construction
Now let's prove these two constructions.
Proof of Simple Construction 1: P inside circle I
Angle OPA is a right angle (by construction). Angle OAP' is also a right angle (by construction). Triangle OPA is similar to triangle OAP' since they share angle AOP' and by AA similarity. We know that corresponding sides in similar triangles are proportional. Since m(OA) = r, we have the proportion m(OP)/r = r/m(OP'). Rearranging this equation gives r2 = m(OP) * m(OP'). This is the definition of inversion. Thus P' is indeed the inverse point. (EOP)
Proof of Simple Construction 2: P outside circle I
Angle OAP is a right angle since it is inscribed in a semicircle. Angle OP'A is also a right angle**. Triangle OP'A is similar to triangle OAP since they share angle AOP and by AA similarity. We know that corresponding sides in similar triangles are proportional. Since m(OA) = r, we have the proportion m(OP)/r = r/m(OP'). Rearranging this equation gives r2 = m(OP) * m(OP'). This is the definition of inversion. Thus P' is indeed the inverse point. (EOP)
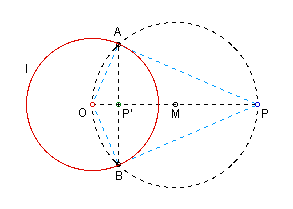
**Proof that angle OP'A is a right angle.
Angle OAP and angle OBP are right angles since they are inscribed in semicircles. So triangles
OAP and OBP are right triangles. OA and OB are congruent since they are both radii of circle I. OP is congruent to itself. Since we have two right triangles with two equal sides, triangles OAP and OBP are congruent. So AP and BP are congruent. Since AP and BP are congruent and OA and OB are congruent, OAPB is a kite by definition. OP and AB are the diagonals of kite OAPB. Since the diagonals of a kite form right angles, angle OP'A is a right angle.
Interesting Properties of Inversion:
We've looked at inverting points, but what about inverting other geometric objects, such as lines and circles? Using the power of Geometer's Sketchpad, we can create the locus of the points on a line or circle inverted in our inversion circle. Then, we can come to some conclusions about the inversions of lines and circles.
Inverting Lines:
Open this sketch in GSP: Inverting A Line
The red circle is the inversion circle. The blue line is the line that we are inverting. The green object is the inverted line (the image of the blue line after inversion). You can change the position of the blue line by clicking on the line and moving it. Notice what happens to the green image as you move the blue line. You can change the slope of the blue line by clicking on the blue point and moving it. Again, notice what happens to the green image as you change the slope of the blue line. You may also want to move or change the size of the red circle (the inversion circle). You can change the position of the red circle by clicking on the circle and move it. You can change the size of the red circle by clicking on the red point on the circle and moving it. Notice what happens to the green image as you change the position and size of the inversion circle.
Inverting Circles:
Open this sketch in GSP: Inverting A Circle
The red circle is the inversion circle. The blue circle is the circle that we are inverting. The green object is the inverted circle (the image of the blue circle after inversion). You can change the position of the blue circle by clicking on the circle and moving it. Notice what happens to the green image as you move the blue circle. You can change the size of the blue circle by clicking on the blue point on the circle and moving it. Again, notice what happens to the green image as you change the size of the blue circle. You may also want to move or change the size of the red circle (the inversion circle). You can change the position of the red circle by clicking on the circle and move it. You can change the size of the red circle by clicking on the red point on the circle and moving it. Notice what happens to the green image as you change the position and size of the inversion circle.
IMPORTANT: Do not read this section until you have fully explored the inversion of lines and circles from above.
Here are the conclusions you should have reached about the inversion of lines and circles....
Conclusions Regarding The Inversion Of Lines
- A line will always invert to either another line or a circle.
- A line through the center of the circle of inversion inverts to itself.
- A line that does not go through the center of the circle of inversion inverts to a circle which does go through the center of the circle of inversion.
- A line that is completely outside the circle of inversion inverts to a circle (that goes through the center of the circle of inversion) that is completely inside the circle of inversion.
Furthermore, the circle will have a radius which is strictly less than one-half the radius of the
circle of inversion.
- A line that is tangent to the circle of inversion inverts to a circle (that goes through the
center of the circle of inversion) that is also tangent to the circle of inversion at the same point of tangency as the original line. Furthermore, the circle will have a radius which is
exactly one-half the radius of the circle of inversion.
- A line that intersects the circle of inversion in two points, but does not go through the
center of the circle of inversion, inverts to a circle (that goes through the center of the circle
of inversion) that intersects the circle of inversion at the same two points as the original
line. Furthermore, the circle will have a radius which strictly greater than one-half the radius
of the circle of inversion.
- A line that is the perpendicular bisector of the radius of the circle of inversion inverts
to a circle that is congruent to the circle of inversion.
- Assume that the original line does not go through the center of the circle of inversion. A
line parallel to the original line that does go through the center of the circle of inversion will
be tangent to the circle created by inverting the original line.
Conclusions Regarding The Inversion Of Circles
- A circle will always invert to either another circle or a line.
- A circle that is orthogonal (the tangent lines are perpendicular) to the circle of inversion
will invert to itself.
- A circle whose center is also the center of the circle of inversion inverts to a circle that
also has the same center. Furthermore, if the original circle is also congruent to the circle
of inversion, then it will invert to itself.
- A circle that contains the center of the circle of inversion inverts to a line that does
not contain the center of the circle of inversion.
- A circle that is completely inside the circle of inversion inverts to either a circle or a line
that is completely outside the circle of inversion.
- A circle that is completely outside the circle of inversion inverts to a circle that is
completely inside the circle of inversion.
References
- Greenberg, Marvin. Euclidean and Non-Euclidean Geometries: Development and
History. Third Edition. W.H. Freeman and Company: New York, 1993.
- Hendon, Maurice. Class notes. MATH 5200: The University of Georgia, Spring 1999.
- Wilson, James. Internet resource: GSP Inversion Script. http://jwilson.coe.uga.edu/EMT669/Essay.Ideas/invert.scrpt.gss .
Return to Home Page



