Notes: Applications of the Pythagorean Theorem and Special Right Triangles

Review from previous day:

Pythagorean Theorem
In a right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the legs.

m<C=90

a^2+b^2=c^2

Here are some examples of word problems that apply the Pythagorean Theorem:

Example 1

A power company employee is going to run a power line from the power pole to the back of Joel's house. Use the drawing below, and determine the approximate length of cable the employee will need.

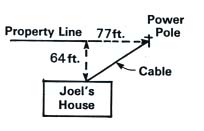
Solution

c^2=a^2+b^2
c^2=(64)^2+(77)^2
c^2=4,096+5,929
c^2=10,025
c=
So c is approximately 100.

Example 2

The length of a rectangle is 24 cm and the width is 10 cm. How long is the diagonal?

Solution

a^2+b^2=c^2
(10)^2+(24)^2=c^2
100+576= c^2
676= c^2
c=
c=26

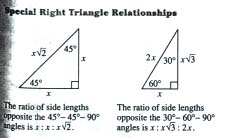
45-45-90 Triangles

A 45-45-90 triangle is an example of a special right triangle. An isosceles right triangle which

means it has two sides of equal length and a 90 angle, has two 45 angles and is called a 45-45-90

triangle. Since we know two sides of the triangle are equal then we also know that the angles

opposite them are equal. You can find the length of the hypotenuse of a 45-45-90 triangle when

the length of a leg is known. Here is a theorem that states how to do this:

The Pythagorean Theorem, which applies to all right triangles, is used to prove the relationships that exist in the 45-45-90 triangle.

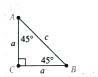
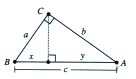
Given: Triangle ABC is a 45-45-90 triangle.

Prove:

Proof: Triangle ABC is a 45-45-90 triangle.

Using the Pythagorean Theorem, a^2+a^2=c^2.

Simplifying, it follows that c^2=2a^2,

Here is an example of a 45-45-90 triangle problem:

Example 3

Find the value of c.

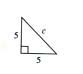
Solution

Example 4

Find the length of the diagonal of a square with side length 12 cm.

Solution

30-60-90 Triangles

A 30-60-90 triangle is another example of a special right triangle that has a 30 degree angle and a

60 degree angle. "The hypotenuse and the longer leg in a 30-60-90 triangle can be found when the

shorter leg is known. The shorter leg is opposite the 30 angle and the longer leg is opposite the 60

angle" (Addison-Wesley Geometry, 313). Here is a theorem that allows you to find the length of

the hypotenuse and the longer leg when the length of the shorter leg is known:

30-60-90 Triangle Theorem

In a 30-60-90 triangle, the length of the hypotenuse is 2 times the length of the shorter leg and the length of the longer leg is times the length of the shorter leg.

The Pythagorean Theorem can again be used to prove the 30-60-90 Triangle Theorem.

Given: Triangle ABC is a 30-60-90 triangle.
Prove: c=2a,

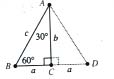
Draw triangle ADC so that triangle ABC is congruent to triangle ADC. When two triangles are

congruent, their angles are equal. So, m<ADB=60 degrees and m<DAB=30 degrees. Therefore,

all three angles of triangle ABD equal 60 degrees. So, triangle ABD is equilateral and hence, c=2a.

Using the Pythagorean theorem, a^2+b^2=c^2. a^2+b^2=(2a)^2=4a^2. Thus, b^2=3a^2. We can simplify to get

Here is an example of a 30-60-90 triangle problem:

Example 5

Find the length of the hypotenuse and the longer leg.

Solution

Hypotenuse: x=2(6)=12

Longer leg: y=

Example 6

Find the length and diagonal length of the rectangle below.

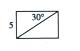
Solution

Diagonal length: c=2(5)=10

Length:

Review: Special Right Triangle Relationships

return to lesson plan