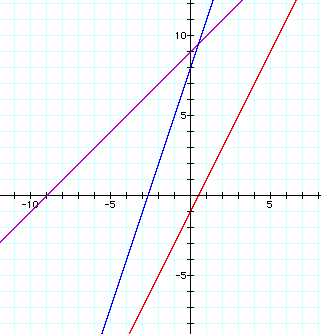
 It
looks like h (x) can be rewritten as 3x-8. If this is true, then
h (x) is also a linear function. Let's look at a general case.
It
looks like h (x) can be rewritten as 3x-8. If this is true, then
h (x) is also a linear function. Let's look at a general case.I want to explore the behavior of three selected linear equations f(x), g(x), and h(x). I want to observe the behavior of these equations when they meet the follow criteria:
For my explorations, I want to set f(x) = x+9 and g(x) = 2x - 1. First I want to look at the equations of f(x), g(x), and h(x) =f(x) + g(x). Here are the graphs of f(x) = x + 9, g(x) = 2x - 1, and h(x) = (x+ 9 ) + (2x - 1).
 It
looks like h (x) can be rewritten as 3x-8. If this is true, then
h (x) is also a linear function. Let's look at a general case.
It
looks like h (x) can be rewritten as 3x-8. If this is true, then
h (x) is also a linear function. Let's look at a general case.
Using the commutative property, this can be rewritten as
Therefpre h(x) = (x + 9) + ( 2x - 1) = 3x + 8 is true. Also true is that h(x) is always linear when you add to linear equations. The slope of h(x) is equal to the sum of the slope of f(x) plus slope of g(x). The y-intercept of h(x) is also equal to the sum of the y-intercept of f(x) plus the y-intercept of g(x). That is
Next, I want to look at the equations of f(x), g(x), and h(x) = f(x) * g(x). Here are the graphs of f(x) = x + 9, g(x) = 2x-1, and h(x) = (x+9) * (2x -1).
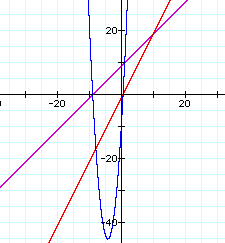
It looks like h(x) can be rewritten as 2x^2 +17x -9. If this is true then h(x) is a quadratic equation. So let's look at the general case.
Using double distributive property or the FOIL method, h(x) can be rewritten as
and using the associative property
since integer addition and multiplication are closed,
and this is the general form od the quadratic equation.
Now I want to look at the equations of f(x), g(x), and h(x) = f(x)/g(x).
Here are the graphs of f(x), g(x), and h(x) = (x+9)/(2x-1).
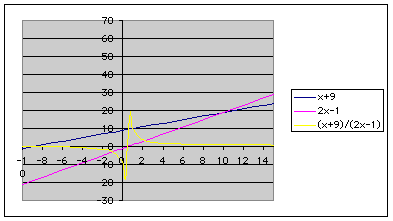
Looking at the graph, h(x) has an asymptote. Where does this asymptote occur? From general knowledge of functions, I know that an asymptote occurs when the equation is discontinous. I know that the equation is discontinous when the denominator is zero becuase division by zero is undefined.
Therefore in this case, h(x) is discontinous when 2x-1 =0. So when does 2x-1 =0?
Let's look at the general case.
Discontinuity occurs when cx+d =0. There is an asymptote in the graph of h(x) at cx+d = 0
Therefore, if h(x) = (ax + b)/ (cx + d), then h(x) will always have a asymptoe at the point where x = -d/c.
Finally I want to look at the equations of f(x), g(x), and h(x) = f(g(x)).
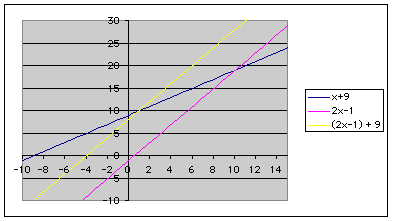
Here are the graphs of f(x), g(x), and h(x) = (2x - 1) + 9.
We can simplify h(x), and then we see that h(x) = 2x - 1 + 9 = 2x + 8. This is also a linear function. Does this always happen? Let's look at the general case.
Multiplication and addition of integers are closed. Then
Then we get h(x) = sx + u, which is the general form of a linear function. Therefore, the compostion of two linears functions is a linear function.