A parametric curve in the plane is a pair of functions
x=f(t)
y=f(t)
where the two continuous functions define ordered pairs (x,y). The two functions are normally called parametric equations of a curve, and the curve is dependent upon the range of t. We will be exploring the parametric equations
as well as variations of these equations. In these cases, t is between o and 2(pi) inclusively.
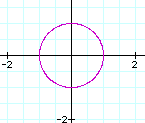
First let's look at the case when

This graph is one that is known to most students as the unit circle. The center is at (0, 0) and the radius is 1. I want to explore what happens to this graph as values in the equation change.
Let's look at the case when something, b is added to cos t. So we now have the situation of
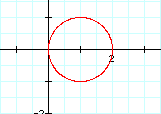
The center of this circle is at (1, 0) and the radius is still 1. So it appears that as b varies in this situation the graph slides along the x-axis. That is the center of the circle is (b, 0) a nd the radius is 1. After further exploration we see that adding c to the sin t function, it slides the circle up and down the y-axis. That is the center of the circle is at (0, c) and the radius is still 1.
Therefore I feel that it is time to generalize.
When we have the equations
then the graphs that we get are circles where the center at (b, c) and radius 1.
More exploration can be done to the graphs by investigating what would happen if we had the functions