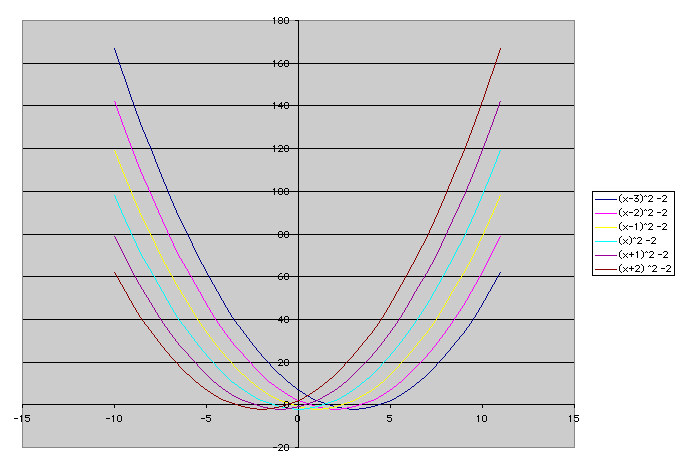
In exploring quadratic functions, I wanted to graph
y = ( x -d)^2 - 2
and see want happens to the graph as d varies.
First I looked at the graph of y = x^2 -2, where d = 0.
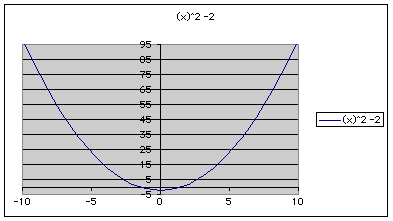
As you see, the graph is a parabola with the vertex at (0, -2).
Let's look at the general case of the vertex form of a quadratic equation.
(d, k) is the vertex of the parabola. For our purposes a = 1 and k = - 2.
So as d varies, the parabola shifts along the x-axis.
So let's look at several graphs of y= (x-d)^2 -2 on the same axes using different values for d, paying close attention to the vertices of each.

It seems that the rule holds that (d, -2) is always the vrtex. The shape does not change, only the position on the x-axis.