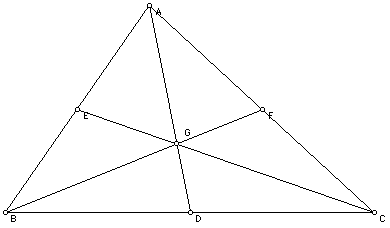
The centroid (G) of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.

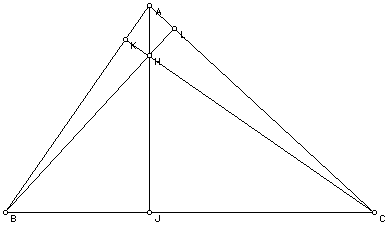
The orthocenter (H) of a triangle is the common intersection of the three lines containing the altitutdes. An altitude is a perpendicular segment from a vertex to the line of the opposite side. H does not have to be on the segments that are the altitudes. In fact, H lies on the lines extended along the altitudes.
The incenter (I) of a triangle is the point on the interior of the triangle that is equidistant form the three sides. Since a point interior to an angle that is equidistant from the two sides of the angle lies on the angle bisector, then the incenter must be on the angle bisector of each angle of the triangle.
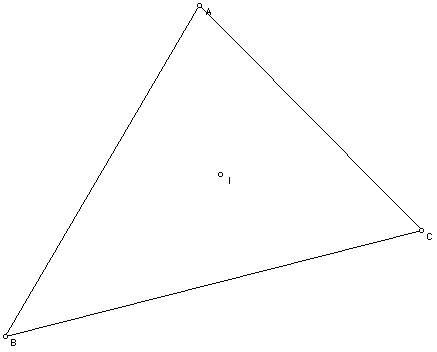
Now we have G, H , C, and I for the same triangle. I want to now look for relationships among them and explore these relationships for the many shapes of triangles (obtuse, right, and acute).
First, let's look at an obtuse triangle.
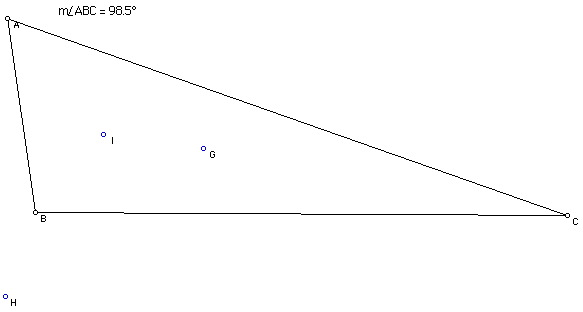
As we notice, the orthocenter is outside of the triangle.
Now let's look at a right triangle.
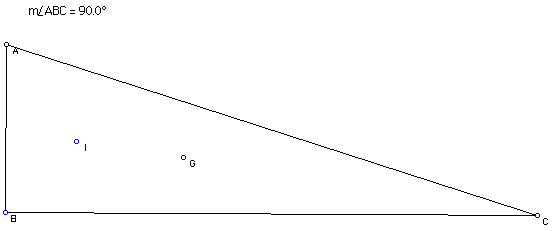
It appears that the orthocenter goes through the vertex and the right angles and I and G stay the same distance apart.
Now let's look at an acute triangle.
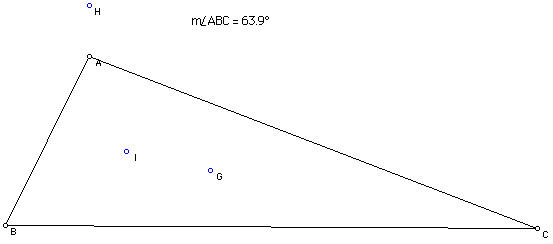
it now appears that the orthocenter has left the interior of the triangle again. This time it exited through vertex A. I and G still appear to be the same distance apart.