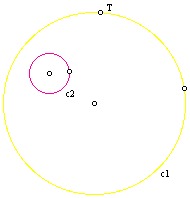
This investigation begins with the following problem.
Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.

We first know that we are given circles c1 and c2 and the point of tangency, which is point T. It is now time to construct our tangent circle.
First I am going to construct a line through the center of c1 goint through point T. Then I am going to construct a circle, where T is the center and has the same radius as circle c2.
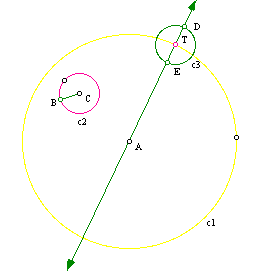
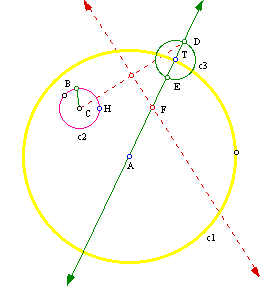
I now want to construct a line segment from point C to point D. After that I wnat to construct the perpendicular bisector of this line segment. The point of intersection will be labeled as point F. The point F will be the center of the tangent circle that we want. Now we can construct this tangent circle we are trying to find using F as the center and FT as the radius.
we now want to look at the construction script for the previous construction of the tangent circle to two given circles. Click here.
We also can construct another tangent circle to the given circles. Instead of constructing a line segment between C anf D, I am going to construct a line segment between C and E.
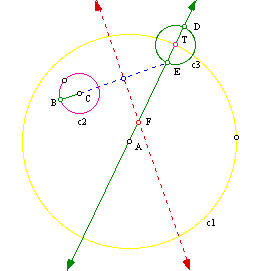
So Fis still the point of intersection and also the circle of the tangent circle with radius of FT.
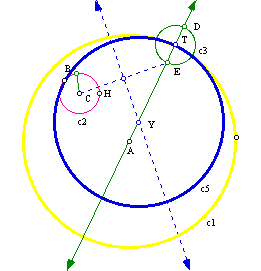
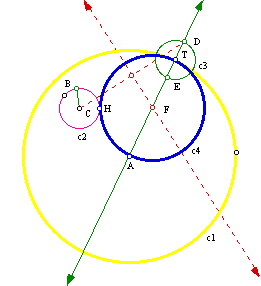
As you will notice this tangent circle is tangent to c2 of the left side and the first tangent circle we got was tangent on the right side. With cues from class discussion and conversation with classmates, I set out to find the locus of the centers of all tangent circles to the given two circles. For this I will use the first construction of tangent circle where the tangent circle was tangent to circle c2 on the right side. As you will notice the locus is an ellipse. Click here to see the animation.