|
|
|
|
The "Golden Triangle" is an isosceles triangle with a vertex angle of 36* and base angles of 72*. The legs are in golden ratio (proportion) to the base. When a base angle is bisected, the angle bisector divides the opposite side in a golden ratio and forms two smaller isosceles triangles. Such Triangles occur in the Pentagram and Decagon (See Figure 1).
Proof: (Looking at Figure 1)

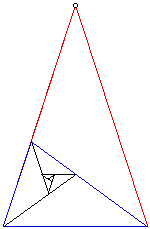
If we take the isoceles triangle that has the two base angles of 72 degrees and we bisect one of the base angles, we should see that we get another Golden triangle that is similar to the first. If we continue in this fashion we should get a set of Whirling Triangles (Figure 2a and 2b).
  |
 |
The bisector of the angle B meets Ac in D, so that D is the golden cut of AC. By this the triangle ABC has been divided into two isoscelestriangles with equal rights to be called "golden," their apex angles being 36* and 108* anfd the ratio of their areas is the golden ratio (phi). Bisecting the angle C we obtain E, the golden cut of BD, and two more golden triangles. This process, producing a series of gnomons, converging to a limiting point O, which is the pole of a logarithmic spiral passing successively and in the same order through the three vertices of each of the series of triangles, ...A, B, C, D, ...
This does not exhaust the intriguing possibilities of the triangle. In addition to the constant recurrence of the golden section, a series obeying the Fibonacci Rule appears in Figure 2b.
If we begin with HG and call it unit lenght, then

Other interesting features can be found in Figure 2b. We have bisected the base angles of successive gnomons. If we join the other bas angles to the midpoints of the sides opposite the, e.g. CX, DY, ..., then
1. The lenghts of these medians form aFibonacci series, and
2. All the medians pass through the pole O.