
You see logarithmic spirals every day. They are the natural growth curves of plants and seashells, the celebrated golden curve of ancient Greek mathematics and architecture, the optimal curve for highway turns. Peer into a flower or look down at a cactus and you will see a pattern of logarithmic spirals criss-crossing each other like so:

This elegant spiral pattern is called phyllotaxis and it has a mathematics that is equally lovely. One reason why the logarithmic spiral appears in nature is that it is the result of very simple growth programs such as
grow 1 unit,
bend 1 unit
grow 2 units,
bend 1 unit
grow 3 units,
bend 1 unit
and so on...
Any process which turns or twists at a
constant rate but grows or moves with constant acceleration will
generate a single logarithmic spiral. An equally similar cellular
automata program will generate phyllotaxis.
The Meristem and Spiral growth patterns
Botanists have shown that plants grow from a single tiny group of cells right at the tip of any growing plant, called the meristem. There is a separate meristem at the end of each branch or twig and it is here that new cells are formed. Once formed, they grow in size, but new cells are only formed at such growing points. Cells earlier down the stem expand and so the growing point rises.
Also, these cells grow in a spiral fashion, as if the stem turns by an angle and then a new cell appears, turning again and then another new cell is formed and so on.
These cells may then become a new branch, or perhaps on a flower become petals and stamens.
The amazing thing is that a single fixed angle can produce the optimal design no matter how big the plant grows. So, once an angle is fixed for a leaf, say, that leaf will least obscure the leaves below and be least obscured by any future leaves above it. Similarly, once a seed is positioned on a seedhead, the seed continues out in a straight line pushed out by other new seeds, but retaining the original angle on the seedhead. No matter how large the seedhead, the seeds will always be packed uniformly on the seedhead.
And all this can be done with a single
fixed angle of rotation between new cells?
Yes! This was suspected by people as early as the last century.
The principle that a single angle produces uniform packings no
matter how much growth appears after it was only proved mathematically
in 1993 by Douady and Couder, two french mathematicians.
You will have already guessed what the
fixed angle of turn is - it is Phi cells per turn or phi turns
per new cell.
The Equiangular Spiral and Shell Spirals
We can make another picture showing the
Fibonacci numbers 1,1,2,3,5,8,13,21,.. if we start with two
small squares of size 1 next to each other. On top of both of
these draw a square of size 2 (=1+1).
We can now draw a new square - touching
both a unit square and the latest square of side 2 - so having
sides 3 units long; and then another touching both the 2-square
and the 3-square (which has sides of 5 units). We can continue
adding squares around the picture, each new square having a side
which is
as long as the sum of the latest two square's sides. This set
of rectangles whose sides are two successive Fibonacci numbers
in length and which are composed of squares with sides which are
Fibonacci numbers, we will call the Fibonacci Rectangles.
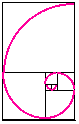
The next diagram shows that we can draw a spiral by putting together
quarter circles, one in each new square.
This is called a golden section spiral or a Fibonacci spiral. A similar curve to
this occurs in nature as the shape of a snail shell or some sea
shells. Whereas the Logarithmic spiral increases in size by a
factor of Phi (1.618..) in a quarter of a turn (i.e. a point a
further quarter of a turn round the curve is 1.618... times as
far from the centre,
and this applies to all points on the curve), the Nautilus spiral
curve takes a whole turn before points move a factor of 1.618...
from the centre. Click on the shell picture (a slice through a Nautilus shell)
to expand it.
I must note that although a golden section spiral (or Fibonacci spiral) is not a true logarithmic spiral they both look alike and it is almost impossible to differentiate between them just by looking. Click here for a nice discussion of this by J. Sharp and click here for a drawing showing the difference between a golden section spiral and a logarithmic spiral.


 `
`Seed heads
Logarithmic Spirals can also be seen in
the arrangement of seeds on flowerheads. Here is a diagram of
what a
large sunflower or daisy might look if magnified. The centre is
marked with a black dot.
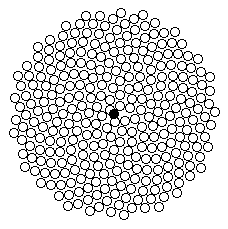
You can see that the seeds seem to form
spirals curving both to the left and to the right. If you count
those
spiralling to the right at the edge of the picture, there are
34. How many are spiralling the other way? You
will see that these two numbers are neighbours in the Fibonacci
series.
The same happens in real seed heads in
nature. The reason seems to be that this forms an optimal packing
of the seeds so that, no matter how large the seedhead, they are
uniformly packed, all the seeds being the
same size, no crowding in the centre and not too sparse at the
edges. If you count the spirals near the centre, in both directions,
they will both be Fibonacci numbers. The spirals are patterns
that the eye sees, "curvier" spirals appearing near
the centre, flatter spirals (and more of them)appearing the farther
out we go.
Here is a quicktime
movie which shows various turns-per-seed
values near phi (0.61803) showing that there are always gaps towards
the outer edge of the "seedhead" and that phi gives
the best value for all sizes of flowerhead.
Pine cones
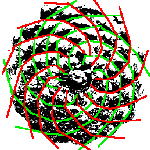
Pine cones show the Fibonacci Spirals clearly. Here is a picture of a pinecone seen from its base (sorry the quality is a bit poor) and another with the spirals emphasised: red in one direction and green in the other.[Click on the images to enlarge them.
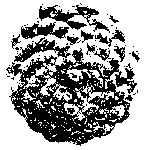
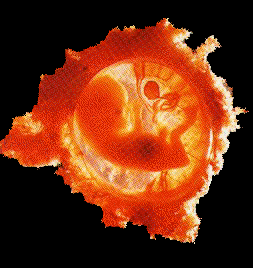
Human Embryo
This is the hardest example of the Equiangular (Logarithmic Spiral) in nature to visualize. If you'll look at the spine, you will see somewhat of a spiral. While this is not exact, it does have a close relationship to the Golden Spiral.
Why does it appear?
The spine lays the foundation for the shape of the rest of the body. Because the spine is designed as a Golden Spiral, it allows for the fetus to take up the least amount of space in comparison to its size. If this were not so, and the embryo were too big, the mother would have much more trouble staying active. This would not be healthy for the mother or her child.
Universe
Look at the beauty of this galaxy and see the equiangular spirals clearly! (At this point I am shocked and this much example is enough to believe)

References:
1. http://www.media.mit.edu/~brand/artist.html
2. H S M Coxeter's Introduction to Geometry, published by Wiley, in its Wiley Classics Library series, 1989
3. http://www.amsci.org/amsci/issues/comsci95/compsci95-05.html
4. http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html
This page created December4, 1999
This page last modified December4, 1999