Pursuit Curve
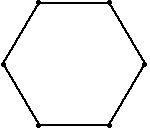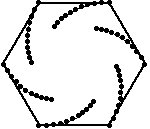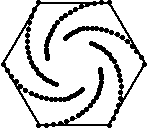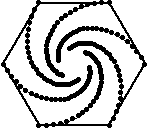
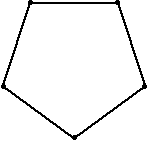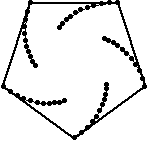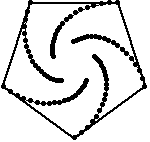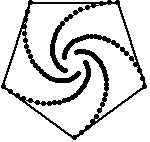
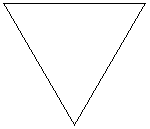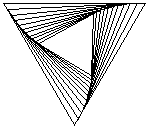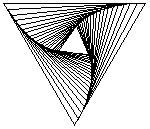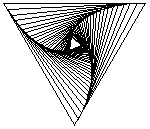
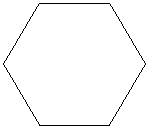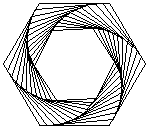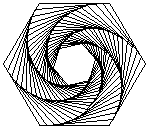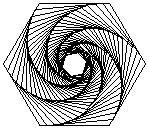
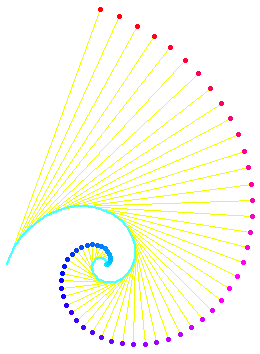
Persuit curves are the trace of an object chasing another. Suppose there are n mice each at a corner of a n sided regular polygon. Each bug crawls towards its next neighbor with uniform speed. The trace of these mice are equiangular spirals of (n-2)/n * Pi/2 radians (half the angle of the polygon's corner). The Figure 1 on the left shows the trace of n mice mice, resulting n equiangular spirals of 45 degree. In the second part of the Figure 1, we may see some whirls which are figures constructed by nesting a sequence of polygons (each haing the same number of sides), each slightly smaller and rotated relative to the previous one. The vertices give the path of the n mice and form n logarithmic spirals.
 |
 |
 |
 |
 |
 |
Catacaustic
Catacaustic of an equiangular spiral with light source at pole is an equal spiral. Proof: Let O be the pole of the curve. Let O' be the reflection of O through the normal of a variable point P on the curve. The locus of O' is then an equal spiral since distance[O,O']/distance[O,P] is constant for any P and equiangular spiral remain unchanged by scaling. Now the reflected ray PO' is just the tangent of O'. End of proof.
|
|
Evolute
The evolute
of an equiangular spiral is an equal spiral, so is its involute.
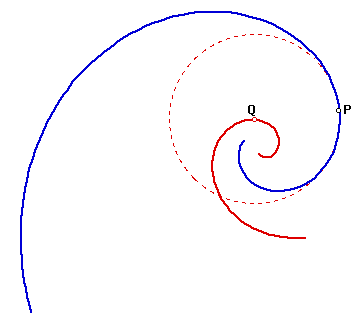
In Figure 3, The left figure shows osculating circles of the curve
and the locus (red curve) of their centers (Q).
The right figure shows the curve's envelope
of normals.
 Figure
3a Figure
3a |
|
|
|
|
Radial
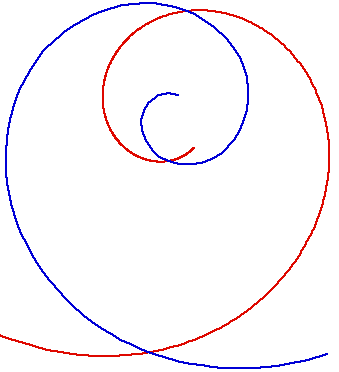
The radial of an equiangular spiral is itself scaled. The Figure 4a shows a 70 degree equiangular spiral and its radial. The Figure 4b shows its involute, which is another equiangular spiral.
|
|
 |
|
|
|
Inversion
The inversion of an equiangular spiral with respect to its pole is an equal spiral (See Figure 5).
 |
Pedal
The pedal of an equiangular spiral with respect to its pole is an equal spiral. In the Figure 6b, the lines from pole to the red dots is perpendicular to the tangents (blue lines). The blue curve is an equiangular spiral. The red dots forms its pedal.
|
|
|
|
|
|
Negative Pedal The negative pedal of an equiangular spiral is shown at Figure 7.
|
|
Parallel
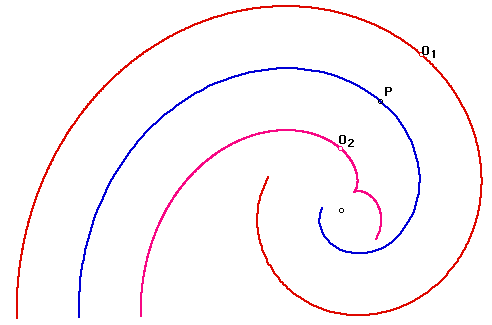
Parallel curves can be defined as the locus of points Q1, Q2 on
the normals of the curve, where Q1 and Q2 are k distant from the
curve (See Figure 8).
 |
Geometric Sequence
If any part of the curve is scale up or down, it becomes congruent to other parts of the curve. Lengths of segments (red lines) cut by equally spaced radii (brown lines) is a geometric sequence. Segments of any radius vector cut by the curve is also a geometric sequence, with a multiplier of E^(2 Pi Cot[alpha]).
|
|
Sources and References:
1. http://www.best.com/~xah/SpecialPlaneCurves_dir/EquiangularSpiral_dir/equiangularSpiral.html
2. http://www.treasure-troves.com/math/whirl.html
3. http://www.treasure-troves.com/math/MiceProblem.html
This page created December 4, 1999
This page last modified December4, 1999