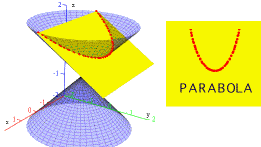

Lesson I: Definition and geometric construction of a parabola
Definition: The parabola is the locus of a set of points equidistant from a fixed point, and a fixed line. The fixed point is called the focus of the parabola and the given line is called the directrix.
|
|
Student Work:
At this point allow students to draw their own sketches on the
computers and observe some properties of the parabola.
After students spend several minutes on observing and playing with the parabola, help students to notice (if they have not noticed) another special point for a parabola: vertex of a parabola.
Teacher's Action: Mark the vertex of the parabola as in the Figure 1. Ask students to determine properties have this special point may have, i.e. the vertex.
Challenge to Students:
What happens if the focus point is under the directrix
instead of above the directrix?
Click here to investigate parabolas on an interactive java applet (If you do not have GSP software on your computer, it's an perfect opportunity to take a look at.)
Lesson II: Introduction to the algebraic representation of a parabola
Before introducing a general equation (i.e. the analytic, polar or parametric form) of a parabola, it is important for them to see the mechanism (or the relation) on the parabola. Simply, the relation between the points on the parabola, the directrix and the focus of the parabola follows from the definition and an application of Pythegorean Theorem.
So before giving a formal equation of a parabola, deal with the following problem:
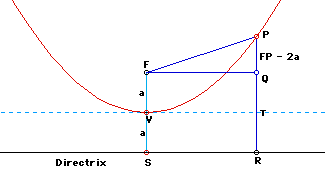
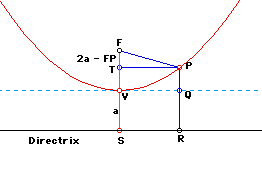
For a parabola the following two cases (See Figure2a and 2b) are valid:
 |
 |
Proof:
In the first case (FS < PR), since FP = PR and FV = VS =a (by the definition of parabola), PQ = FP - 2a. By Pythagorean Thm. applied to the right triangle FPQ,

The second case (FS > PR) is left for students' own investigations and constructions.
Lesson III: Analytic Equation of a Parabola
Let's put a coordinate system so that the vertex of the parabola is the origin of the parabola and the parabola opens upward (See Figure 3).
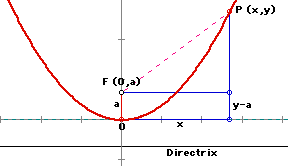 |
As we did above, since the distance between focus and the parabola is equal to the distance between the point and the directrix:
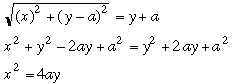
Thus the general equation of the parabola with vertex at the origin (0,0) and upwards has the general equation
The quantity 4a is known as the Latus
Rectum. If the vertex is at ![]() instead
of (0, 0), the equation of the parabola is
instead
of (0, 0), the equation of the parabola is
Similarly, for a parabola opening to the right with vertex at (0, 0) (See Figure 4), the equation in Cartesian Coordinates is
|
|
If the vertex is at ![]() instead of (0, 0), the equation of the parabola is
instead of (0, 0), the equation of the parabola is
If we expand the equations
![]() &
&![]()
We may write a very general equation of a parabola in cartesion coordinate system is
Lesson IV: Understanding the simplest parabolas
of the form ![]()
The lesson is located at: http://jwilson.coe.uga.edu/EMT668/EMAT6680.F99/Erbas/write-ups/AKEwrite-up2/AKEwrite-up2.html
Lesson V: Polar and Parametric Equations of a Parabola
In Polar Coordinates, the equation of a parabola with parameter a and center (0, 0) (See Figure 5) is:
|
|
Using the definition of the parabola, since the distance between the center (0,0) and the point is equal to the distance between the point and the directrix,
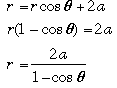
Parametric Form: The parametric equations of a parabola are
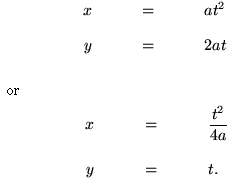
Students work in groups and each student makes his/her own electronic portfolio of the solutions and investigations.



Lesson VII: Reflective (Optical) Property of Parabola
If a ray of light travels perpendicular to the directrix of a parabola (or in three dimensions, a paraboloid of revolution) and strikes the concave side of the parabola, then it will be reflected to the focus. Equivalently, if a ray of light leaves the focus and strikes the parabola, it will be reflected in a path perpendicular to the directrix (See Figure 6a & Figure 6b). This property is an essential feature of satellite dishes, car headlights, radio telescopes, and reflecting telescopes, including liquid mirror telescopes. In fact, if you throw a ball, it will follow a parabolic path.
|
|
|
|
To investigate the reflective property with java technology, here is an opportunity:
Students' Investigation: An interesting property can be observed when one looks at the locus of a point on the reflected ray that is a fixed distance from the Point P that moves along the parabola. In Figure 7, we see the locus (thick blue curve) of the point x on reflected ray as P moves along the parabola. GSP file allows one to examine the locus for various distances of the point x from P. Since the reflected ray passes through the focus, the locus for any X will be symmetric.
|
|
Here are some other similar curves for different X points on the reflected ray.
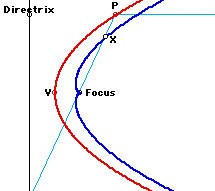
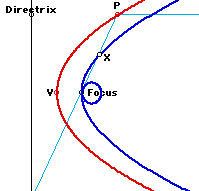
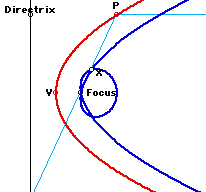
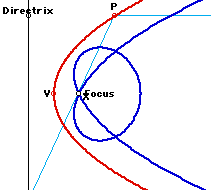
Lesson VIII: Properties of tangents to a parabola
Let V be the vertex of a parabola. And let the line L be perpendicular to the directrix of the parabola at V. For a point A on L, if AC is constructed, where IAVI = IBVI, then AC is tangent to the parabola (See the figure below)
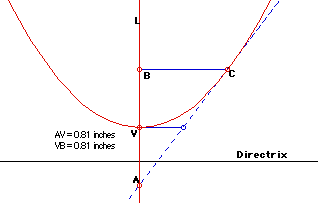
Click here for GSP sketch and a formal proof.
Lesson IX: Area property of a parabola
This lesson investigates the ratio between the area of the parabolic section bounded by a parabola and a chord and the area of the triangle which has the vertex of the parabolic section and two points of intersection of the segment and the parabola as its vertices
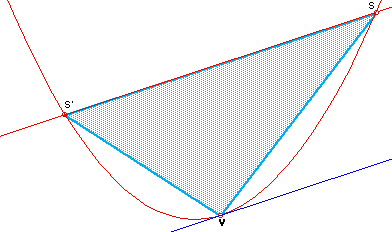
Click Here for the lesson and related investigations
Students' prepare and present a project dealing with parabolas. This could be individual or group work. The project subjects could be the applications of parabolas in daily life, more advanced properties of parabolas, or more detailed versions of the classroom investigations.
