

| This theorem has been noted as one of the most surprising theorems in elementary geometry. It was discovered in 1899 by Frank Morley, and it was not until ten years after it had arrived that two proofs were given. One was trigonometric in nature and was given by M. Satyanarayana, and the other was more of an elementary proof given by M. T. Naraniengar. | A statement of the theorem:
|
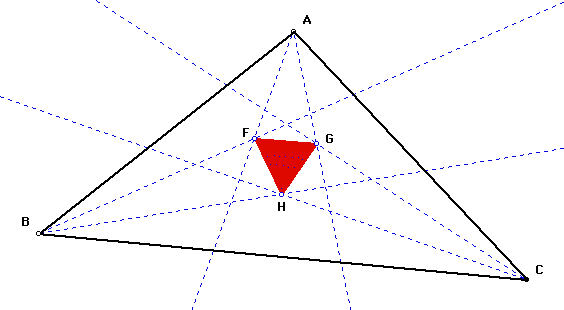
To put this theorem in other words, any triangle ABC yields an equilateral triangle FGH if the angles A, B, and C are trisected by rays AF and AG, BF, and BH, CH, and CG. (See diagram below) Early attempts to prove this theorem showed that a direct approach brings in too many difficulties, and that a better way to work this problem is to start with an equilateral triangle and work backwards. While doing research on this problem, I have found many other proofs for this theorem, including some direct ones. See the links at the bottom of this document for more information on these proofs.
Geoff's Page | Morley Main Page | Morley Proof Page