Problem: Find two linear functions f(x) and g(x) such that their product, h(x) = (f(x))(g(x)), is tangent to each of f(x) and g(x) at two distinct points. Discuss and illustrate the method and the results.
Suppose f(x) = ax + b and g(x) = cx + d.
Then, h(x) = acx^2 + (ad + bc)x + bd.
We will consider the case in which the coefficient of x equals zero (i.e., ad + bc + 0). Therefore h(x) = acx^2 + bd = ac(x - 0)^2 + bd is a parabola whose vertex is at (0,bd) and whose line of symmetry is x = 0.
We make the following assumptions and observations:
1. h(x) is an even function. That is, h(x) = h(-x).
2. For the purposes of this investigation, we will assume that c is the additive inverse of a. Thus, g(x) = -ax + d.
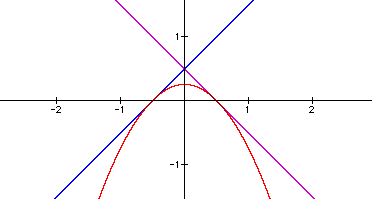
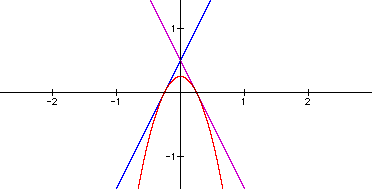
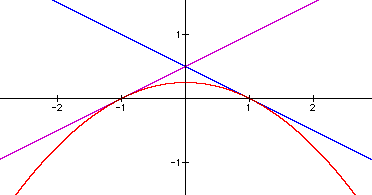
3. Since ad + bc = 0 and c = -a, ad + b(-a) = 0. That ad = ba implies that d = b. So, f(x) = ax + b, g(x) = -ax + b and h(x) = -a^2(x^2) + b^2.
4. h(x) and f(x) intersect at the points (-b/a, 0) and ((b - 1)/a, 2b - 1). If h(x) is tangent to f(x) at one point, then these ordered pairs must be one and the same. Setting the x-coordinates equal to each other, we find that b = 1/2. So, f(x) = ax + 1/2, g(x) = -ax + 1/2, and h(x) = -a^2(x^2) + 1/4. The vertex of the parabola is (0, 1/4).
5. h(x) is tangent to f(x) at the point (-1/2a, 0), and h(x) is tangent to g(x) at the point (1/2a, 0)
6. f(x) intercepts the x-axis at (-1/2a, 0), g(x) at (1/2a, 0). Note that these also are the points of tangency.
7. The two linear functions intersect at the point (0, 1/2).
8. So, (ax + 1/2)(-ax + 1/2) must equal -a^2(x^2) + 1/4, and h(x) must be tangent to the two linear functions f(x) and g(x) at two distinct points.
Using Graphing Calculator, we plug in different values of a to show that, given the parameters we have imposed, the parabola h(x) is tangent to lines f(x) and g(x), and (f(x))(g(x)) = h(x). This statement is true for all real values of a. The following are three illustrations, substituting the values 1, 2, and -1/2 for a.