The Spreadsheet in Mathematics Explorations

by

Ralph Hickman

 

This is an exploration of data provided by the lumber industry comparing the age of a forest with the approximate number of board feet of lumber which can be gotten from each tree. We will attempt to produce a function that fits the data and predict numbers of board feet for forests of other ages.

Tree Data

Age of Tree

100s of Board Feet
   

20

1

40

6

60

--

80

33

100

56

120

88

140

--

160

182

180

--

200

320

We first suppose that the increase in the number of board feet (dy) during a certain period is proportional to the number of board feet at the beginning of the period (y) and to the duration of the period (dt). That is, dy = ky(dt) or dy/dt = ky.

We solve the differential equation dy/dt = ky, letting y = y0 when t = 0.

dy/y = k(dt).

Integral[dy/y] = Integral[k(dt)].

ln(y) = kt + C.

At t = 0, C = ln(y0). Therefore,

ln(y) = kt + ln(y0).

ln(y) - ln(y0) = kt.

ln(y/y0) = kt.

y/y0 = e^kt.

y = y0(e^kt).

We measure time in units of 20 years, beginning at age 20. Thus, y0 = 1 and y180 = 320. So,

320 = 1(e^k(180)).

ln(320) = 180k.

ln(320)/180 = k.

0.032046228 = k.

Therefore, y = 1(e^(0.032046228t)) is the function we now evaluate.

The following table shows the numbers of board feet of lumber generated by substituting the tree ages into our function. Use of a spreadsheet program enables us to visually compare the results with what we know to be true.

Tree Data Derived from the Function y = e^(0.032046228t)

Age of Tree

100s of Board Feet
   

20

1

40

1.898

60

3.603

80

6.840

100

12.984

120

24.646

140

46.784

160

88.808

180

168.578

200

320

Here are the graphs of the data provided by the tree industry (Series 1) and the data yielded by our function (Series 2):

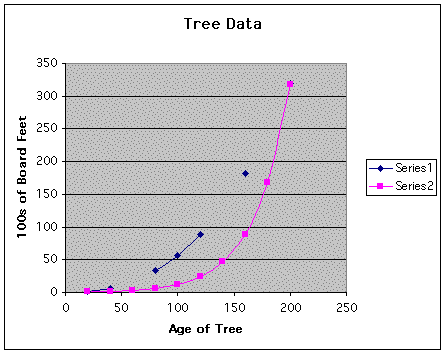
The graph reveals that the exponential function y = e^(0.032046228t) is not an accurate model of the given data.

Suppose that the function we seek is a power function. We hypothesize that the number of board feet which a tree can yield is proportional to the square of the age of the forest (i.e., the age beyond an established starting point) plus 1. The age at which our measurement begins is 20 years. So, the function is y = k(t - 20)^2 + 1. Again, let y0 be the number of board feet at t0 = 0. Thus, y0 = 1 and y180 = 320. So,

y180 = k(200 - 20)^2 + 1.

320 = k(180^2) + 1.

k = 319/(180^2) = 0.009845679.

Our function is y = 0.009845679(t - 20)^2 + 1.

Here are the data table for this function and its graph:

Tree Data Derived from the Function y = 0.009845679(t - 20)^2 + 1

Age of Tree

100s of Board Feet
   

20

1

40

4.938

60

16.753

80

36.444

100

64.012

120

99.457

140

142.778

160

193.975

180

253.049

200

320

In the following graph, Series 1 represents the data provided by the lumber industry, Series 2 the data yielded by our function.

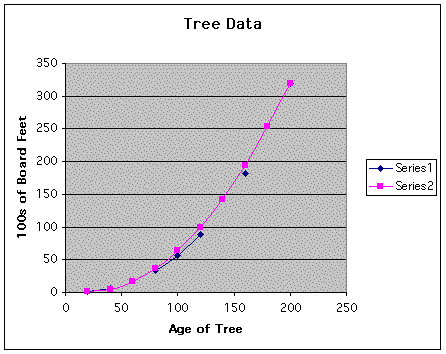
We see that the function y = 0.009845679(t - 20)^2 + 1 much more closely models the data with which we were provided. Using this function, we can approximate the number of board feet for ages 60, 140, and 180 years, and we can estimate the number of board feet for trees greater than 200 years old.

f(60) = 16.753.

f(140) = 142.778.

f(180) = 253.049.

f(220) = 394.827.

f(240) = 477.531.

f(300) = 772.901.

Application of the goodness of fit test reveals that the function y = 0.009845679(t - 20)^2 + 1 is not an extremely accurate model of the data. The measure of error is 50.264. Refinement of the function is required, but is not here attempted.

Return