

The following is an overlay of graphs of the equation
for b = -3, -2, -1, 0, 1, 2, and 3. (The intersection of the graphs is the point (0, -4).)
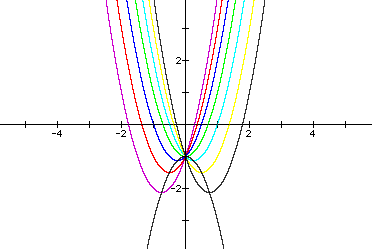
The vertex of each parabola occurs where the tangent to the curve is horizontal (i.e., where 4x + b = 0). Solving for b, we see that b = -4x. Substituting this value for b in the original equation shows that y = 2x^2 + (-4x)x - 4 = -2x^2 - 4. Thus, the locus of the vertices is the parabola
In fact, the locus of the vertices of all y = ax^2 + bx + c, where a and c are fixed and b is a variable element of the set of integers, is the parabola y = -ax^2 + b.
We now solve the equation ax^2 + bx + c = 0 for each coefficient.
If we hold x constant, then the graphs of the three equations are one-and-the-same plane in three-space.
Letting x equal 1 yields the following:
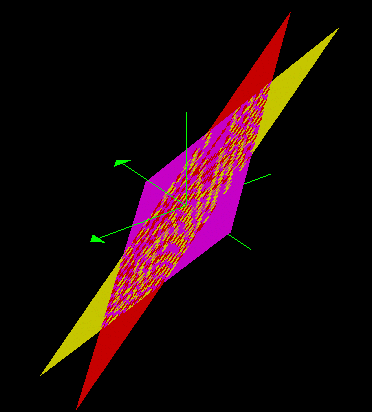
The violet plane represents a = -b - c; the red represents b = -a - c; the yellow represents c = -a - b. It is clear that all are equivalent to the plane a = -b - c.
The value of the graph is that it identifies the real values of coefficients a, b, and c which satisfy the equation ax^2 + bx + c = 0 when 1 is a real root.
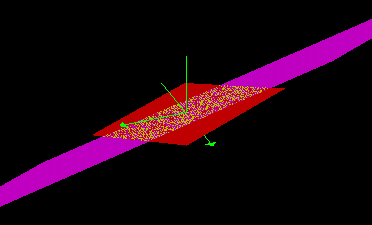
Here is the graph when x = -(1/2). The coefficients which satisfy a(1/4) + b(-1/4) + c = 0 generate the plane a = ((b/2) - c)/(1/4).
When x = 0, the coefficients of ax^2 + bx + c = 0 generate the plane c = 0.
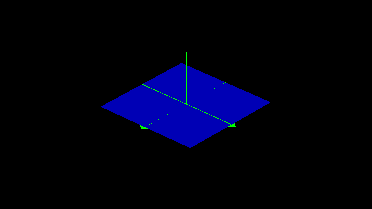
So, if we know that x is a nonzero, real root of ax^2 + bx + c = 0, then the coefficients a, b, and c are coordinates which determine the plane a = (-bx - c)/x^2.