

Problem: Given two vertices X and Y of triangle XYZ and the angle at the third vertex Z (i.e., the angle opposite side XY), find the locus of the point Z.
Solution:
1. Construct the circumcircle of XYZ. Construct radii OX, OY, and OZ.
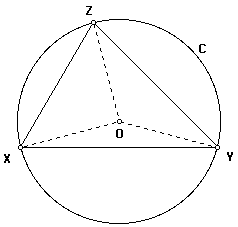
2. d(OX) = d(OY) = d(OZ).
3. d(OY) = d(YO) [Distance is symmetric.] By the Isosceles Triangle Theorem, since d(OX) = d(YO), then m(OXY) = m(XYO). Now, m(OXY) + m(XYO) + m(YOX) = 180. [Triangle Angle Sum Theorem] So, 2m(OXY) + m(YOX) = 180. In the same manner, it can be shown that 2m(OYZ) + m(ZOY) = 180 and 2m(OZX) + m(XOZ) = 180.
4. By the Triangle Angle Sum Theorem, m(ZXY) + m(XYZ) + m(YZX) = 180. Since angle measure is additive, m(ZXY) = m(ZXO) + m(OXY), m(XYZ) = m(XYO) + m(OYZ), and m(YZX) = m(YZO) + m(OZX). Thus, we can say that 2m(OXY) + 2m(OYZ) + 2m(OZX) = 180.
5. We know that m(YOX) + m(ZOY) + m(XOZ) = 360. Therefore,
m(YOX) = 360 - m(ZOY) - m(XOZ)
m(YOX) = 360 - (180 - 2m(OYZ)) - (180 - 2m(OZX))
m(YOX) = 2(m(OYZ) + m(OZX))
6. From (2.), m(YZX) = m(YZO) + m(OZX). But, m(YZO) = m(OYZ); so, m(YZX) = m(OYZ) + m(OZX).
7. Therefore, m(YOX) = 2m(YZX). In fact, for any point H on circle C on the same side of chord(XY) as Z, with H not Z, m(YOX) = 2m(YHX). [Z and H are on the same side of chord(XY) if and only if the proper angle measure of XYZ and the proper angle measure of XYH have the same sign.]
8. The length of segment(XY) is constant; so, m(YOX) is constant. Thus, we conclude that the locus of point Z is the major arc of angle(YOX).
Click here to view an animation of point H.
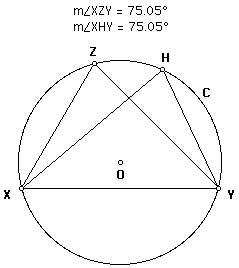
Question: What happens to the measure of angle YHX when H and Z are on opposite sides of chord(XY).