

This is an investigation of circles which are tangent to two intersecting circles. We consider the case where two given circles C1 and C2 intersect at two distinct points.
I. To construct tangent circles on the interiors of C1 and C2:
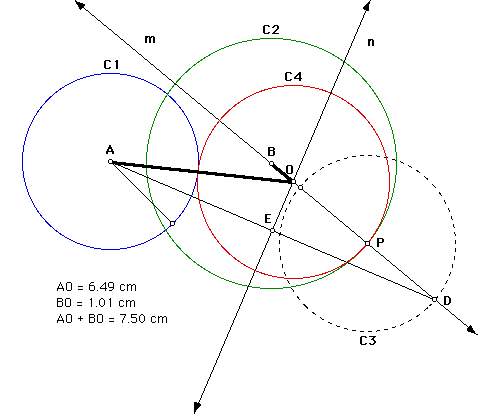
1. Let points A and B be the centers of C1 and C2, respectively. Let P be an arbitrary, initial tangent point on C2.
2. Construct a line m through the center of C2 which contains this point.
3. Construct a circle C3 with center P and radius equal to that of C1. The point of intersection D of the line m and C3 on the exterior of C1 is the endpoint of segment(AD).
4. Construct the midpoint E of segment(AD) and a line n perpendicular to AD at that point.
5. The point of intersection O of lines m and n is the center of a circle C4 which is tangent to both C1 and C2.
Geometer's Sketchpad can be used to investigate what happens to the tangent circle C4 as the arbitrary point P is moved around C2. Click here to view an animation.
When P is on the exterior of C1, the tangent circle is on the interior of C2 and on the exterior of C1. When P is at a point of intersection of circles C1 and C2, the tangent circle vanishes. As P travels through the interior of C1, the tangent circle is on the interior of C1 and on the exterior of C2.
By viewing the animation, we see that the locus of the centers O of the tangent circles is an ellipse with foci A and B. Thus, the sum of the distances from point O to points A and B is constant.
II. To construct tangent circles on the exterior of C1 and C2:
(This construction is based on an exploration performed using Geometer's Sketchpad.)
1. Construct the points of intersection D and E of circles C1 and C2. Construct the line w through D and E. Let H be an arbitrary point on w.
2. Construct segments AH and BH and their midpoints J and K, respectively. Construct circle C3 by center J plus point H and circle C4 by center K plus point H.
3. Let F be the point of intersection of C1 and C3, and let G be the point of intersection of C2 and C4. We observe that H is a point of intersection of C3 and C4.
4. Construct line u through F and H and line v through G and H. u is tangent to C1 at F; v is tangent to C2 at G. (Why?) Construct line x, which contains points A and F, and line y, which contains points B and G. Since segment(AF) is a radius of C1 and u is a tantent line, x is perpendicular to u at F. Similarly, segment(BG) is a radius of C2, and v is a tangent line; thus, y is perpendicular to v at G.
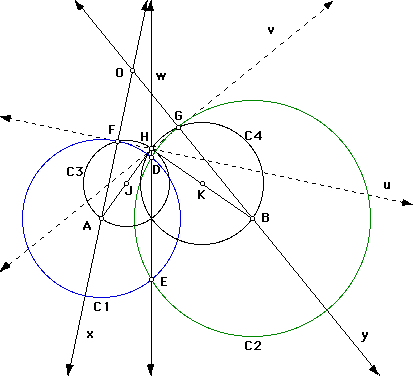
5. The point of intersection O of lines x and y is the center of a circle tangent to C1 and C2. An animation of H along line w shows that the locus of the centers O of the tangent circles is a portion of a hyperbola with foci A and B. (Click here to view the animation.) By definition, the absolute value of the difference of the distances from point O to points A and B is constant.
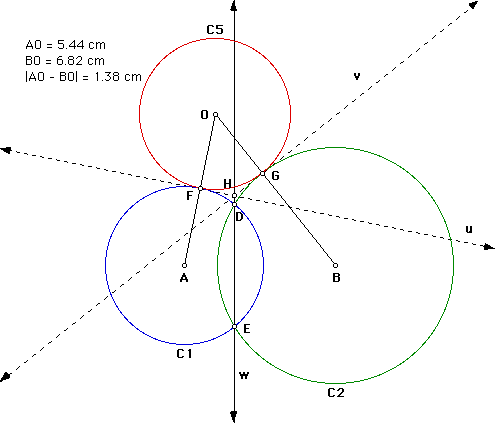
6. Note: Performing the above construction by establishing an arbitrary point W' on w on the opposite side of segment(AB) produces another set of tangent circles, the locus of whose centers completes the hyperbolic curve.