

Problem: The internal angle bisectors of triangle ABC are extended to meet the circumcircle at points L, M, and N, respectively. Find the angles of triangle LMN in terms of the angles A, B, and C.
Solution: The following diagram illustrates the construction of triangles ABC and LMN.
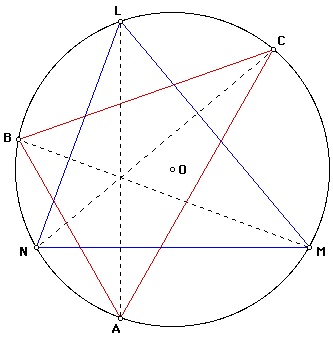
We begin by constructing segments from the center O of the circumcircle of triangle ABC to the vertexes of the two triangles. (Point O is also the center of the circumcircle of triangle LMN.) Let X be the point of intersection of segments BC and OL, Y the point of intersection of segments CA and OM, and Z the point of intersection of segments AB and ON.
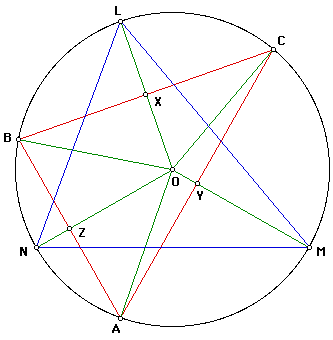
We claim (1) that segment(OL) is perpendicular to segment(BC), (2) that segment(OM) is perpendicular to segment(CA), and (3) that segment(ON) is perpendicular to segment(AB). An investigation of these claims using Geometer's Sketchpad reveals that the perpendicular bisectors of the sides of triangle ABC contain points L, M, and N. (See the following diagram.) By the definition of the circumcircle of triangle ABC, point O also is on the three bisectors.
Segments OL and BC each contain points X and X'. Since O, L, B, and C are distinct points and since O and L are not collinear with B and C, it follows that segments OL and BC intersect at one point. That X and X' are held by both segments implies that X = X'. We conclude also that Y = Y' and that Z = Z'.
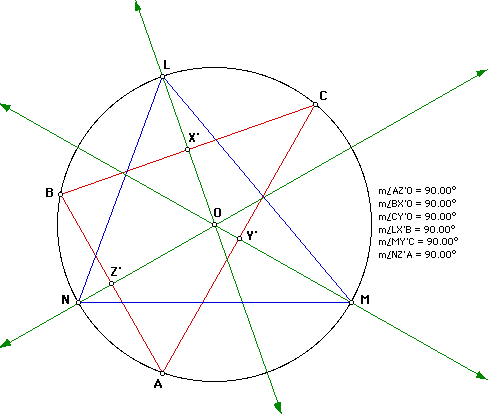
We know that, by the definition of a circle, d(OA) = d(OB) = d(OC) = d(OL) = d(OM) = d(ON). Therefore, triangles OAC, OBA, and OCB are isosceles.
We now make use of a theorem which states that the line drawn from the vertex of an isosceles triangle to the midpoint of the opposite side bisects the angle at the vertex and is perpendicular to the opposite side. That line(OM) bisects segment(CA) at point Y implies that m(AOY) = m(YOC). Using the same arguement we can show that m(BOZ) = m(ZOA) and that m(COX) = m(XOB). Since angle measure is additive, m(AOY) + m(YOC) = m(AOC), m(BOZ) + m(ZOA) = m(BOA), and m(COX) + m(XOB) = m(COB).
To find the solution to our problem, we recall the following theorem about circles: The measure of an inscribed angle is equal to half the measure of the central angle of its intercepted arc. Thus, the measure of the inscribed angle CAB is equal to half the measure of the central angle COB. (The intercepted arc of angle CAB is the set of all points W on the circumcircle such that ray(AW) is between ray(AC) and ray(AB).) So, m(CAB) = (1/2)m(COB) = m(COX) = m(XOB). The measure of the inscribed angle ABC is equal to half the measure of the central angle AOC; so, m(ABC) = (1/2)m(AOC) = m(AOY) = m(YOC). And, the measure of the inscribed angle BCA is equal to half the measure of the central angle BOA; so, m(BCA) = (1/2)m(BOA) = m(BOZ) = m(ZOA).
Continuing this line of reasoning, we see that the measure of the inscribed angle NLM is equal to half the measure of the central angle NOM. Now, m(NOM) = m(NOA) + m(AOM) = m(ZOA) + m(AOY) = m(BCA) + m(ABC). [Angle measure depends only on rays.] So, m(NLM) = (1/2)[m(BCA) + m(ABC)].
The inscribed angle LMN is equal to half the measure of the central angle LON. Now, m(LON) = m(LOB) + m(BON) = m(XOB) + m(BOZ) = m(CAB) + m(BCA). So, m(LMN) = (1/2)[m(CAB) + m(BCA)].
The inscribed angle MNL is equal to half the measure of the central angle MOL. Now, m(MOL) = m(MOC) + m(COL) = m(YOC) + m(COX) = m(ABC) + m(CAB). So, m(MNL) = (1/2)[m(ABC) + m(CAB)].
Thus, the solution of the problem is as follows:
Angle L = (1/2)(angle C + angle B),
angle M = (1/2)(angle A + angle C), and
angle N = (1/2)(angle B + angle A).