

Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F, respectively.
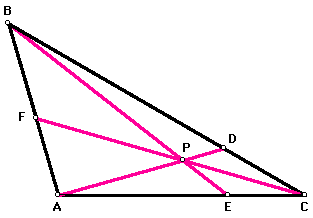
An examination of the products (AF)(BD)(CE) and (FB)(DC)(EA) using Geometer's Sketchpad (GSP) shows that the two are equal. This equality holds when the figure is constructed in such a way that line AP intersects line BC at point D, line BP intersects line CA at point E, and line CP intersects line AB at point F. Thus, when P is outside triangle ABC, segments AF, BD, CE, FB, DC, and EA are maintained, and the relation between the two products is retained.
Click here to view a GSP document in which you can move point P both within and without triangle ABC and observe the equality of the two products.
We claim that the following is true: (Area(AFP))(Area(BDP))(Area(CEP)) = (Area(FBP))(Area(DCP))(Area(EAP)).
Consider the following diagram:
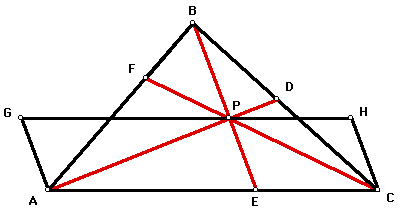
Triangles CEP and EAP are, to quote Euclid, "in the same parallels" AC and GH. (Euclid, 1956a, p. 333) Thus, they have the same height. In his Proposition 1, Book VI of the Elements, Euclid (1956b) states, "Triangles and parallelograms which are under the same height are to one another as their bases." (p. 191) Therefore, the area of triangle CEP is to the area of triangle EAP as the length of segment CE is to the length of segment EA. That is, Area(CEP)/Area(EAP) = (CE)/(EA).
Similarly, Area(AFP)/Area(FBP) = (AF)/(FB), and Area(BDP)/Area(DCP) = (BD)/(DC). Given that (AF)(BD)(CE)/(FB)(DC)(EA) = 1, we conclude that (Area(AFP))(Area(BDP))(Area(CEP))/(Area(FBP))(Area(DCP))(Area(EAP)) = 1. Hence, (Area(AFP))(Area(BDP))(Area(CEP)) = (Area(FBP))(Area(DCP))(Area(EAP)), as required.
Again, this relation holds when point P is outside triangle ABC. Click here to view a GSP document in which you can move point P both within and without triangle ABC and observe that this is so; or, click here to view the relation as P travels around the circumcircle of triangle ABC.
We now investigate the ratio of the areas of triangle ABC and triangle DEF when P is inside triangle ABC. Let X be the point of intersection of lines DP and EF, Y the point of intersection of lines EP and FD, and Z the point of intersection of lines FP and DE.
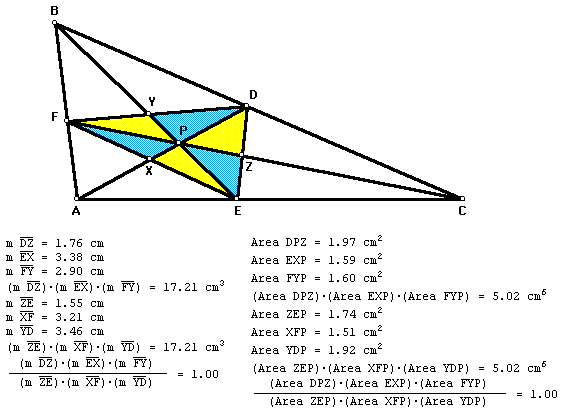
Points X, Y, and Z were constructed as were points D, E, and F of triangle ABC. So, the qualities of triangle DEF are those of triangle ABC. Thus, (DZ)(EX)(FY)/(ZE)(XF)(YD) = 1, and (Area(DZP))(Area(EXP))(Area(FYP))/(Area(ZEP))(Area(XFP))(Area(YDP)) = 1.
By Euclid's Proposition VI.1, (AP)/(XP) = Area(EAP)/Area(EXP). Hence, Area(EXP) = Area(EAP)[(XP)/(AP)]. Likewise, (AP)/(XP) = Area(AFP)/Area(XFP). Hence, Area(XFP) = Area(AFP)[(XP)/(AP)]. By the same argument, we can show that Area(FYP) = Area(FBP)[(YP)/(BP)], Area(YDP) = Area(BDP)[(YP)/(BP)], Area(DZP) = Area(DCP)[(ZP)/(CP)], and Area(ZEP) = Area(CEP)[(ZP)/(CP)].
The area of triangle DEF equals the sum of the areas of the six smaller triangles which comprise DEF. Thus, Area(DEF) = [Area(EAP) + Area(AFP)][(XP)/(AP)] + [Area(FBP) + Area(BDP)][(YP)/(BP)] + [Area(DCP) + Area(CEP)][(ZP)/(CP)].
Investigation with GSP reveals that the area of triangle DEF is maximized when point P is the centroid of triangle ABC (i.e., when DEF is the medial triangle of ABC). Since the area of a medial triangle is one-fourth the area of its parent triangle, it follows that DEF is maximized when the ratio of the areas of ABC and DEF is equal to 4.
Now the rays extending from the vertices of triangle ABC through the midpoints of their opposite sides divide ABC into six smaller triangles of equal area. (Our strategy for proving this would rely upon a repeated application of the proposition that "triangles which are on equal bases and in the same parallels are equal to one another." (Euclid, 1956a, p. 333)) In addition, rays AD, BE, and CF bisect the sides of the medial triangle DEF, thus dividing DEF into six smaller triangles of equal area.
So, we have that the area of each one of the six triangles which comprise triangle DEF (e.g., triangle EXP) is one-sixth the area of DEF or (1/6)(1/4)Area(ABC). That is, Area(EXP) = (1/24)Area(ABC). That Area(EXP) = Area(EAP)[(XP)/(AP)] implies that (1/24)Area(ABC) = (1/6)Area(ABC)[(XP)/(AP)]. Therefore, (XP)/(AP) = 1/4. In the case where DEF is the medial triangle, (XP)/(AP) = (YP)/(BP) = (ZP)/(CP) = 1/4.
Returning to the equation for the area of triangle DEF, Area(DEF) = [Area(EAP) + Area(AFP)](1/4) + [Area(FBP) + Area(BDP)](1/4) + [Area(DCP) + Area(CEP)](1/4) = (1/4)[Area(EAP) + Area(AFP) + Area(FBP) + Area(BDP) + Area(DCP) + Area(CEP)] = (1/4)Area(ABC). This confirms that, when the area of triangle DEF is maximized, the ratio of the area of triangles ABC and DEF is 4.
We conclude that, in the general case, this ratio is greater than or equal to 4. Click here to view a GSP document in which you can move point P to the centroid position (point G) and other locations and observe this ratio.