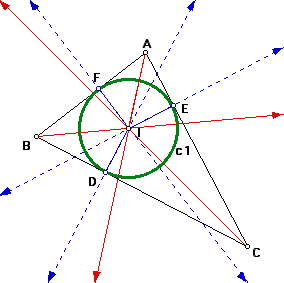
The Gergonne Point was discovered by and named after Joseph Diaz Gergonne. The theorem goes as follows: the segments from the vertices of a triangle to the points of tangency of the incircle with the opposite sides of the triangle are concurrent. This point of concurrency is called the Gergonne point. The proof can be done easily by using Ceva's Theorem.
Proof: See Figure 1 below. Let c1 be the incircle (green) of triangle ABC, and let point I be the center of c1, or incenter of the triangle. Recall that the incenter is the point of concurrency of the angle bisectors (red) of a triangle. Also, that the incircle is formed by constructing lines (blue) through point I perpendicular to the sides of the triangle. The points where these lines intersect the sides of the triangle (points F, D, and E) are the points of tangency of the incircle.

Notice triangles AFI and AEI (figure 2). Angle AFI and AEI are both right angles, and angle FAI = angle EAI because of the angle bisector. Since angle AFI = angle AEI, and angle FAI = angle EAI, then angle FIA = angle EIA. The length of side AI = the length of side IA by the reflexive property. Therefore, triangle AFI is congruent to triangle AEI by angle-side-angle congruency. So, AF = AE.
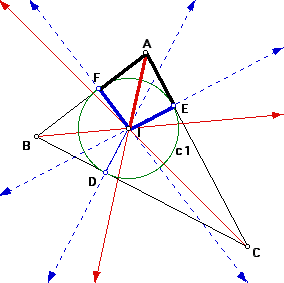
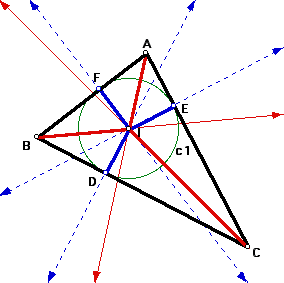
The same argument is used to prove that BF = BD, and CD = CE. See figure 3.
Now, remember that the Gergonne Point G is the point at which the segments (yellow) from the vertices of the triangle to the points of tangency of the incircle with the opposite sides of the triangle intersect. See figure 4.
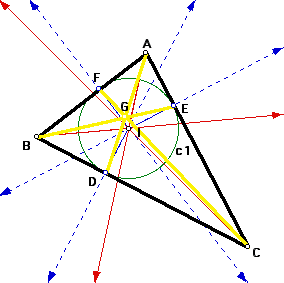
Above, we proved that AF = AE, BF = BD, and CD = CE. Ceva's Theorem states that (AF/BF)(BD/CD)(CE/AE)=1 if and only if segments AD, CF, and BE are concurrent. So by substituting the values, we have (AE/BD)(BD/CE)(CE/AE) = 1. Therefore, AD, CF, and BE are concurrent at G, the Gergonne Point.
Click Here to see a GSP sketch of the Gergonne Point