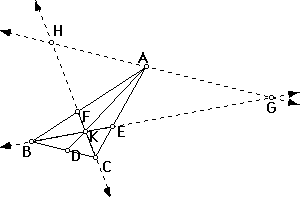
1.) Extend the lines BE and CF beyond the triangle until they meet GH, the line through A parallel to BC (see Figure 2). There are now several pairs of similar triangles: AHF and BCF, AEG and BCE, AGK and BDK, CDK and AHK (where K is the intersection point of AD, BE, and CF). From these triangles in that order we have the following ratios:
a. AF/FB=AH/BC
b. CE/EA=BC/AG
c. AG/BD=AK/DK
d. AH/DC=AK/DK

2.) From c and d we conclude that AG/BD=AH/DC,
and after doing a little algebra, we have:
e.) BD/DC=AG/AH.
Now multiplying a, b, and e we have
AF/FB*BC/DC*CE/EA=AH/BC*BC/AG*AG/AH=(AH*BC*AG)/(BC*AG*AH)=1
So, if the lines AD, BE, and CF intersect at the point K, then
AF/FB*BD/DC*CE/EA=1 holds. So the fact that AD, BE, and CF intersect
at one point is sufficient for this condition to hold. We must
now prove that it is not only sufficient but is also necessary.
In other words, we must now prove that if AF/FB*BC/DC*CE/EC holds
then AD, BE, and CF are concurrent.
3.) So assume that K is the point of intersection of BE and CF
and draw the line AK until its intersection with BC at a point
D'. Then, from part 1 of the theorem, we haveAF/FB*BD'/D'CA*CE/EA=1.
However, it is given that AF/FB*BD/DC*CE/EA=1.So combining the
two we have (BD'+D'C)/D'C=(BD+DC)/DC. This gives us BD'/D'C +1=BD/DC
+ 1 or BD'/D'C=BD/DC. Finally we have BC/D'C=BC/DC which implies
that D'C=DC. So D' and D are the same point and the proof is complete.