Y=ASIN(BX+C) and Its Graph

By Carolyn Johnson

University of Georgia

 

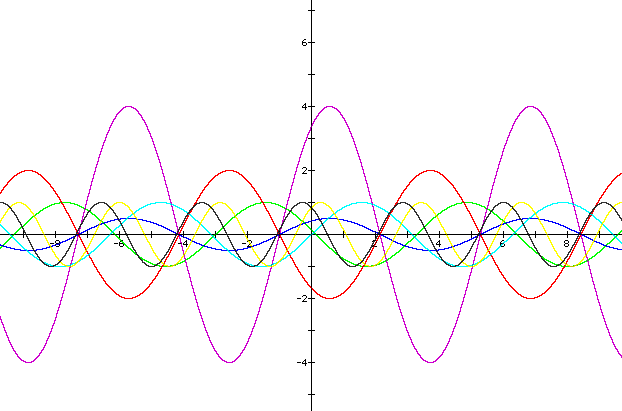
For my first assignment I chose to examine the graph of y = asin(bx + c) when various values are given for a, b, and c. The reference graph (the one showing all the examined graphs) is as follows:

It's very colorful but hard to examine altogether such as this. So let's examine each one individually.

 

Y= Sin (x)

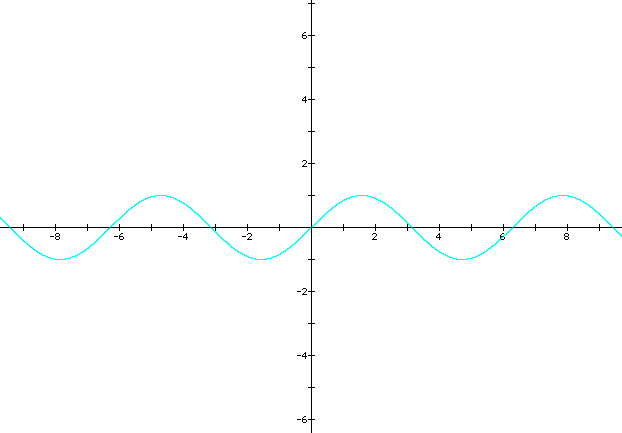
We will first look at the basic equation of y = 1sin( 1x + 0), otherwise y = sin(x) The graph is represented by the color blue. The graph begins at the point ( 0, 0 ) and travels through a period of 2pi, repeatedly. The range is confined to ( -1, 1 ).

Y = Sin (x + 3)

Next we look at the graph of y = sin(x + 3). Here the value for c is 3 while a and b remain at one. The color for this graph is green. The range of ( -1, 1) still remains the same. The difference of this graph compared to the basic one is that the graph is shifted three units to the left of the original point of origin.

Y = 4Sin (x + 1)

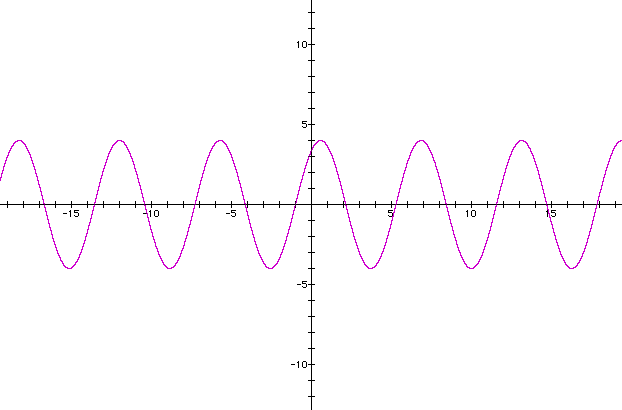
Let us see what happens if we keep b and c constant at one (with the exception of the last equation) and vary the values for a. For the first graph with a = 4, the representive color is purple. The graph is shifted to the left one unit because of the ( x + 1), but the most prominent difference is the height of the graph. The range has increased from the original ( -1, 1 ) to the range of ( -4, 4 ) The period has remained the same.

Y = 0.5 Sin(x + 1)

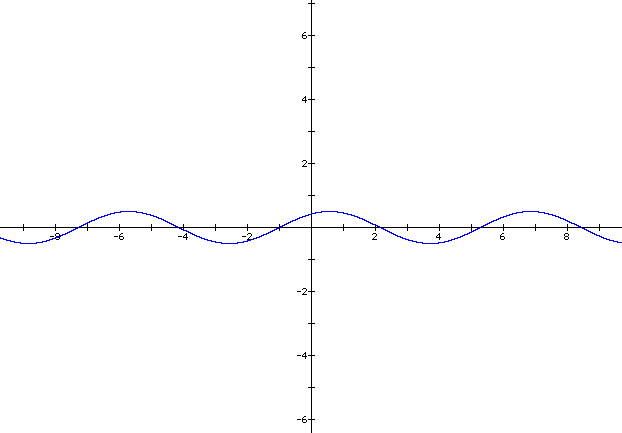
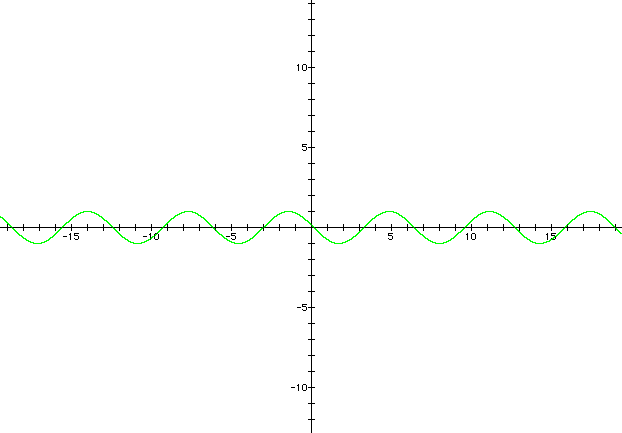
When a = .5, with b and c equal to one, the graph (represented by the color dark blue) has its range of ( -.5, .5 ).

 

Y = -2 Sin (x + 1)

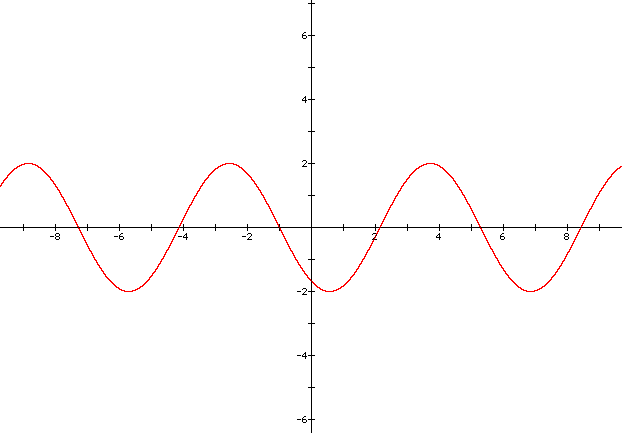
When a = -2, the range is increased to ( -2, 2), but its most noticeable difference is that it is reflected around the x-axis (red graph).

After examining these three graphs we see that the coefficient a affects the altitude of the graph, that is its the range. Values greater than one increases the altitude. Values less than one decreased the altitude, while negative values cause the graph to be reflected around the x-axis.

 

Y = Sin (2x + 1)

Y = Sin (-2x + 1)

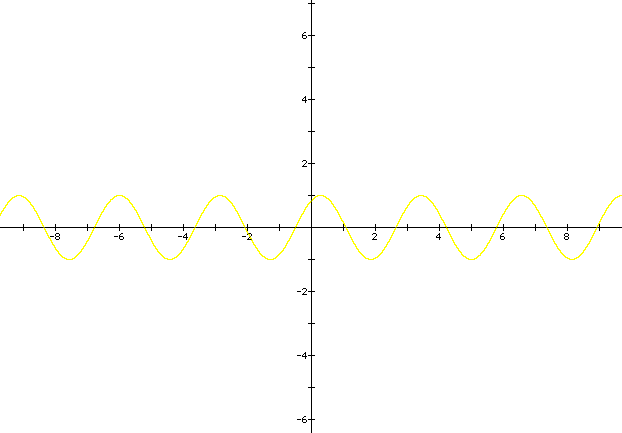
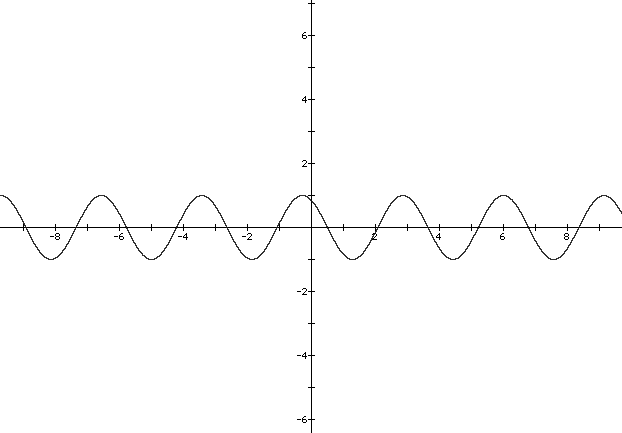
Now we will examine what happens when the value for b is varied. When b = 2, (graph shown in yellow) it causes the graph to be shifted one half an unit to the left. Therefore the -2 would cause the graph to shift to the right (in black).

The shifting mentioned above is the result of the part of the equation (bx + c). We need the x to have the coefficient of one, therefore we would have b(x + c/b). With " + c/b" the graph would be shifted to the left of the point of origin (0, 0). With "-c/b" we would shift the graph to the right of the origin.

So we see that a, b, and c do affect a graph in its own way.

 

 

RETURN