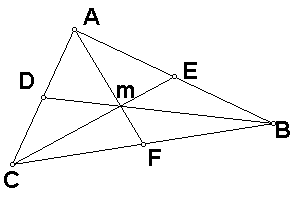
Of the various centers of triangles, I have chosen to examine the centroid center. The centroid is the point of intersection of the three concurrent medians of the triangle. A median is the line segment that extends from a vertex to the midpoint of the opposite side. After constructing a median from each vertex to the opposite midpoint, the three lines intersect at only one point, that point being the centroid.

Let's look at how the centroid center reacts when the vertices are reconstructed in various ways.
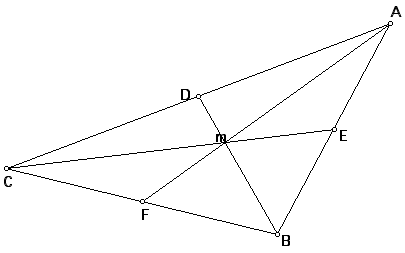
In the above graph the vertex A was mainly shifted to the right. That move did not seem to affect "m" very much. Let's shift again.
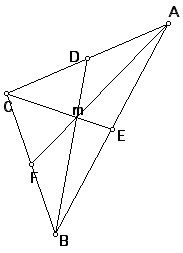
This time vertex "B" was primarily shifted. So far the movement has not affected the center very much. Let's do it again.

Again A is moved, but this time A is pulled downward. The sides of the triangle are coming closer to "m", but "m" is still central to the vertices.

Now there is a noticable change! All three sides come together to form a straight line. What happened to "m"? It is on the straight line along with the other points D, B, E, A, F, and C.

Notice now that vertex B is at the top of the triangle to the right side of vertex C. The center "m" is STILL inside the triangle. Can we ever get the center to lie outside of the triangle? Let's look at some other graphs to see.

Not yet!

Still not yet!

I thought that maybe if C were at the top we might could finally get "m" outside of that triangle. No such luck. One more try!

I've made the triangle small, big, elongated, flat, with the vertices every which way, and I STILL couldn't make the centroid center move outside of its triangle. Must be that the centroid center will always remain within the perimeters of its triangle. Well, I tried!