One benefit of using the program GSP in solving geometric problems is the ease of changing, rearranging, exploring different values without all the erasing and wasting of paper and patience. The following problem was solved with the assistence of GSP.
A 4 by 4 picture hangs on a wall such that its bottom edge is 2 feet above your eye level. How far back from the picture should you stand, directly in front of the picture, in order to view the picture under the maximum angle?
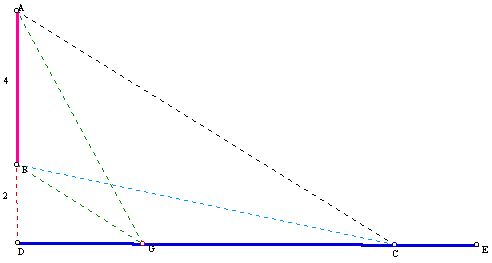
This is the side view of the problem:

The bottom blue line represents the "eye level", the pink vertical line represents the picture, and the angle ABC is the angle we want maximized. The idea is to get angle ACB to be the greatest measurement of degrees for optimal viewing of the picture. Let's go into our GSP animation to see where the greatest angle for viewing will be located. Click Here.
So you can see as point C moves along the bottom line, the greatest measurement for angle ACB is 28.35 degrees, located at point G on the bottom line. Theoretically, this should be the spot to stand on for maximum viewing of the picture. The distance from the picture to point G is 10.39 feet. (This was calulated using the sine of angle AGD and the Pythagorean Theorem).
Another interesting aspect of this point G is that it is also the point of tangency of the line and the circle as well as the optimal point of viewing the picture.
