
Given two circles and a point on one of the circles, construct a circle tangent to the two circles with one point of tangency being the designated point.
This is our problem to explore. Remember that to be tangent to another circle, the two circles must have only one point in common, meaning that they touch each other only at one point. The following graph is the basis for our exploration.

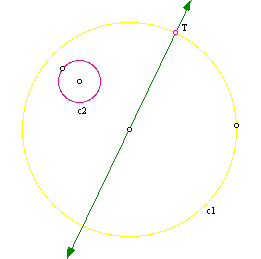
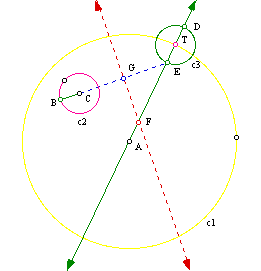
We have our two given circles, c1 and c2, and the point of tangency, pointT. With our givens we will work toward the construction of our tangent-circle.
(1) Construct a line through the center of c1, going through the point T.
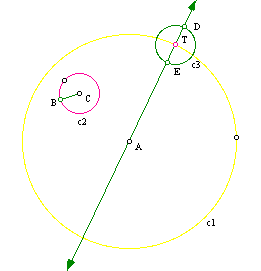
(2) Construct a circle c3 with point T as its center and having the same radius as c2
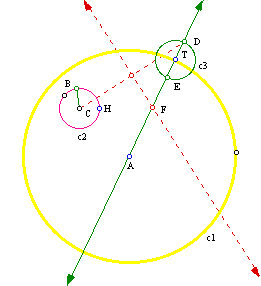
(3) Construct a line segment from point C to point D. Then construct the perpendicular bisector of that line segment. Next locate the point of intersection, point F, of the perpendicular bisector line and the line throught point A of circle c1.
(4) The point F is the center of the tangent circle we have been trying to get. Draw a circle having point F as the center and segment FT as the radius.
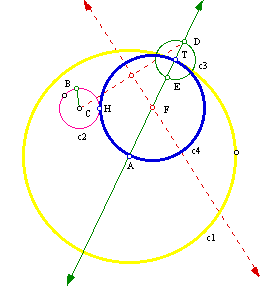
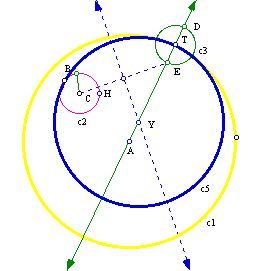
We can easily find another tangent circle with the set-up we have now. This time draw the line segment from point C to pointE, find the perpendicular bisector, and the point of intersection of the bisector and the line through point A.
Now we construct the tangent circle c5 by using point Y as the center and YT as the radius. This time the tangent circle is tangent to c2 on its other side.
Now we'll use animation with our first set of tangent circles (c1, c2, c3, and c4) to find the locus of the centers of all possible circles tangent to our two given circles, c1 and c2. Tracing the locus will show an interesting aspect of the locus. Let's go to animation to see what we can find.

What is happening with our graph? As it moves around a strange red line is being drawn! Don't panic. That is just the "locus" of the centers of the tangent circles. That means, it is the drawing representing of all the centers of the circles that are tangent to our original given circles. What does the locus look like? After making a complete tracing, the locus is in the form of an ellipse. So the locus is an ellipse with its foci at the centers of the original given circles. Very interesting!