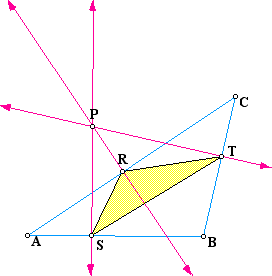
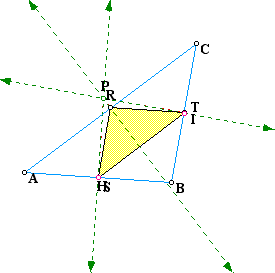
For this assignment we are to find the "pedal triangle" for the "pedal point P." Triangle ABC is an arbitrary triangle with point P being any point in the plane. Perpendicular lines are then constructed from point P to each of the sides of triangle ABC. Points R, S, and T are the points of intersection of the perpendicular lines (originating from point P) to the triangle's sides. After connecting R, S, and T with constructed segments, we then have the "pedal triangle" RST. The following graph shows the pedal triangle in yellow.

What happens if the pedal point P is also the centroid of triangle ABC? We would have the following graph. Remember that the centroid is the point of intersection of the triangle's medians.
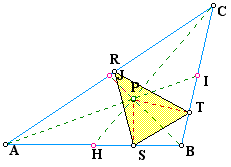
What if the point P is the incenter? It would result in this graph. The incenter is the center of the triangle's incircle (not shown).
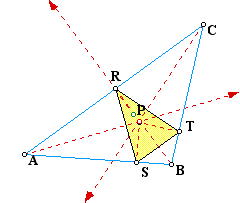
What if the point P is the orthocenter? Notice P and the orthocenter are located outside this triangle. It can exist inside or outside of the triangle just like the orthocenter.
What if P is the circumcenter? This is what we would get. The circumcenter is located outside of the triangle as the orthocenter above. As with the orthocenter, the circumcenter can be located inside or outside the triangle.
What will our graph look like if point P is located at each of the vertices of the triangle ABC?
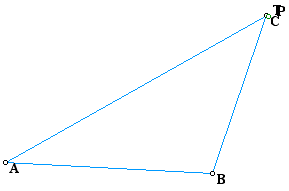
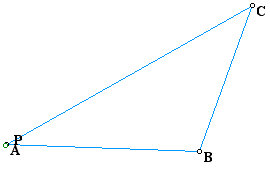
The graph on the left represents Point P at vertex C, while the second graph shows Point P at vertex A. In both instances the pedal triangle's vertices converge to one point, the vertex C and vertex A.
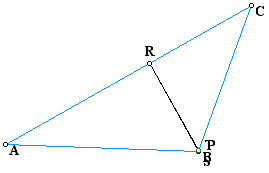
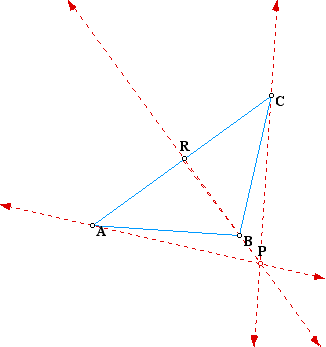
The above graph exhibits the graph when point P is located at the vertex B. In this instance the pedal triangle's vertices are collinear. This line, consisting of the collinear, pedal-triangle's vertices , is called the "Simson Line."