For this assignment we examine parametric curves. A parametric curve in the plane represents a pair of continuous functions that define ordered pairs (x,y). The equations are called the parametric equations of the curve. The range of "t" needs to be large enough so that the whole graph will be completed.
First let's see what the graph looks like when a and b are equal to one.
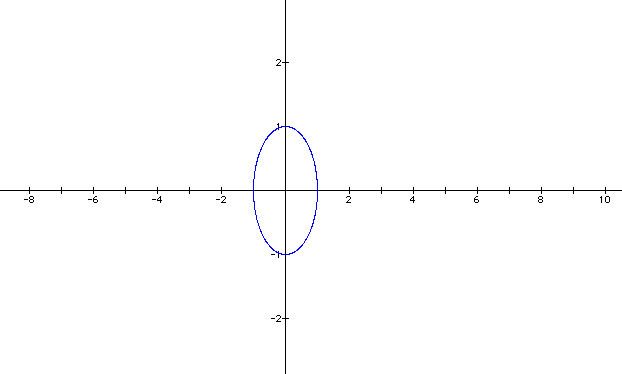
We have a nice ellipse when a and b are equal to one. Now let's see what happens when both a and b equal two.
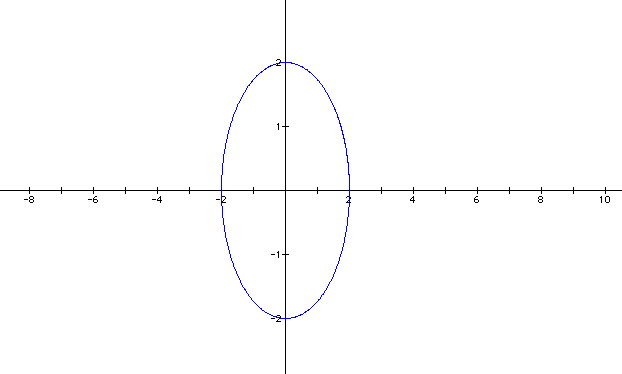
The general shape has remained the same, except it is wider and longer. So let's vary a and b, not having them equal. Set a = 2 and b = 3.
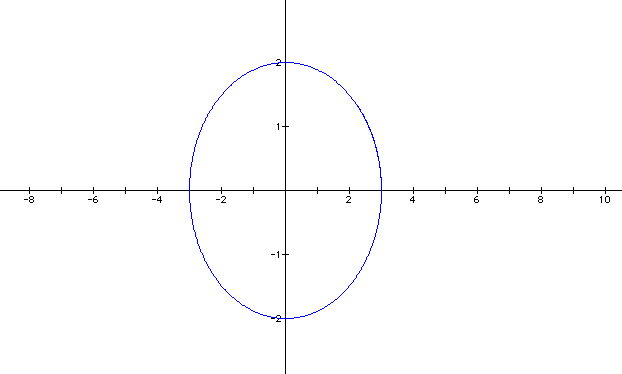
Let's do it again. This time b = 2 and a = 3.
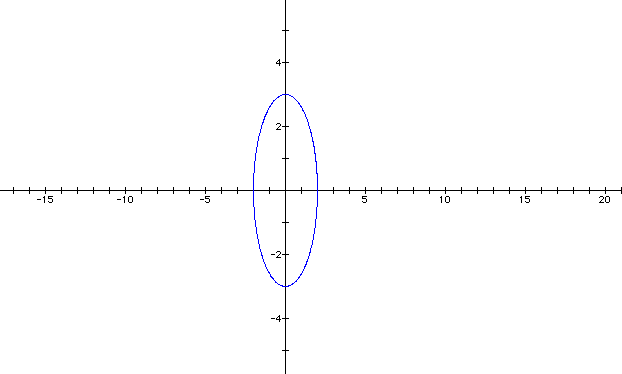
So far it seems that the only thing that a and b change is the graph's width and/or length. I wonder what will happen when a and b are negative numbers. Let a = -2 and b = -3.
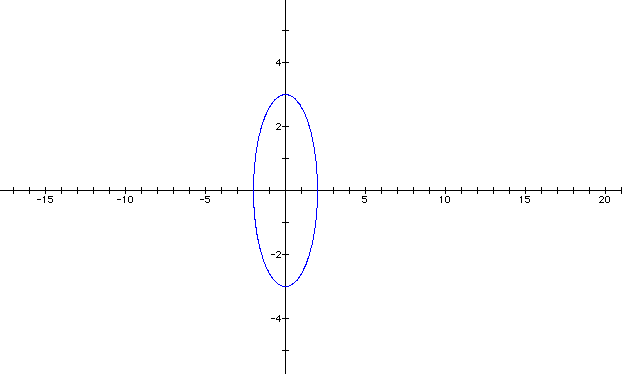
The graph looks the same. Since the positive and negative values of a and b are used in the graphing, starting with a negative value has no ill-effect on the graph.
Let's see what effect there is when a is larger than b. Let a = 5 and b = 2.
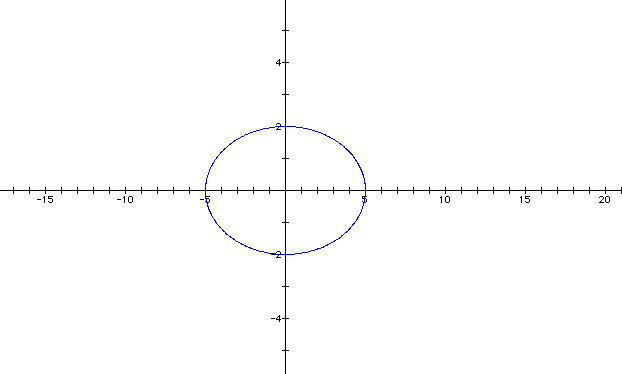
It appears that if a is greater than b the ellipse elongates along the x-axis. If b is greater than a, the graph will elongate along the y-axis.
So for our original equation we see that the variations in a and b, both positive and negative, cause the graph to vary in its width and/or length.
Let's look at another equation that looks
very similar to our original one, but its results are quite different.
The equation is 
. First let a =
2 and b = 3 as we did in the first equation. Let's see what we
get.
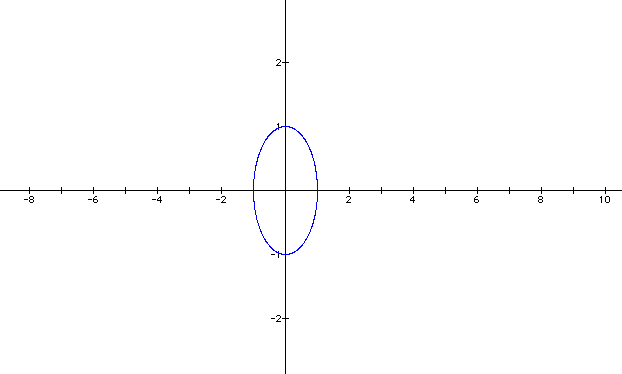
This graph looks like our very first graph when a and b both equaled one. So far there is no indication of the two equations being different. Let's examine further before we generalize that the equations are equivalent. Let's see if there is a difference when a = 2 and b = 3 as we did in the other equation.
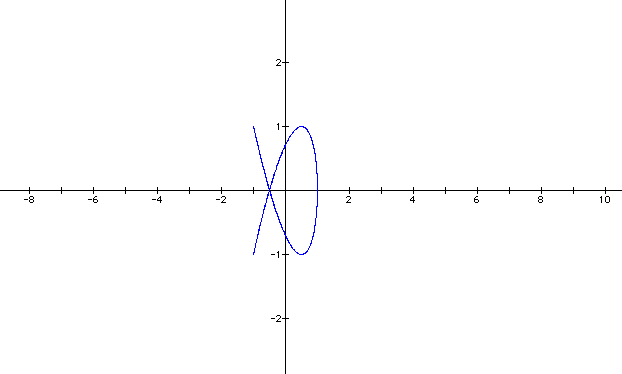
WOW! Now it's different! Let's set a = 3 and b = 2 and see what happens.
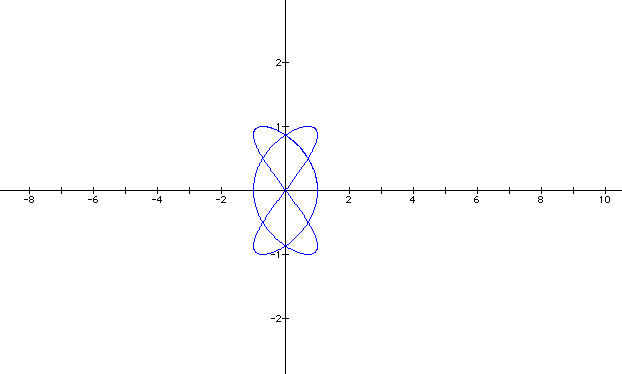
It's definitely different! I like it. Let's explore some more.
Why don't we let a = 4 and b = 5.
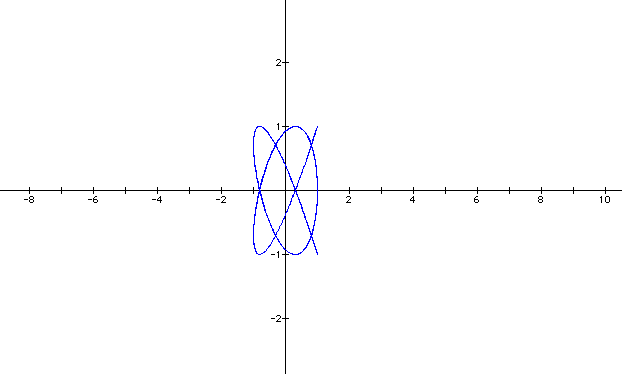
Let a = 6 and b = 2.
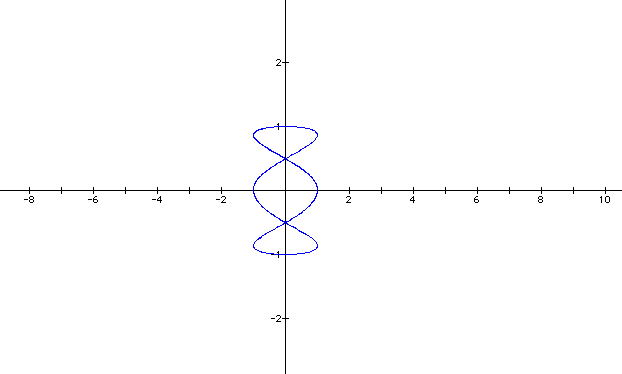
I like it! Now a is set at 4 and b is set at 7.
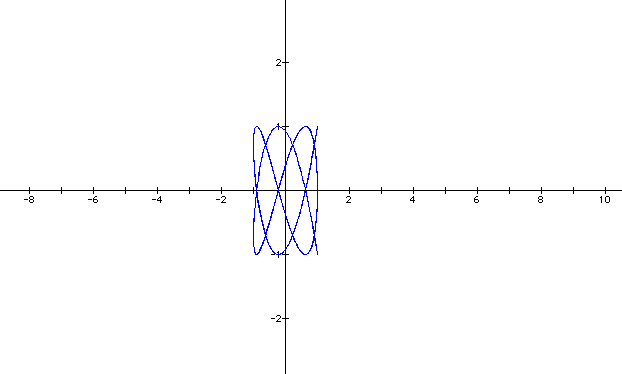
Now let's switch the values around with a = 7 and b = 4.
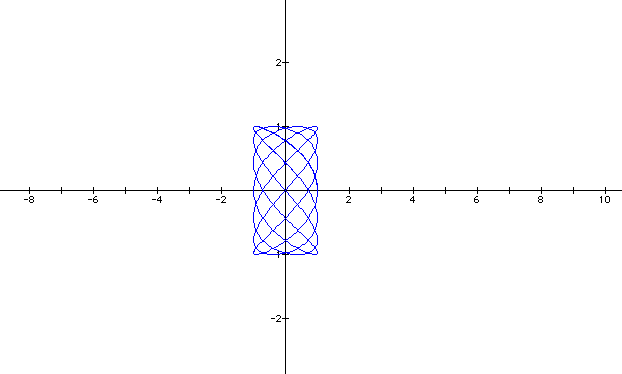
Another neat graph. I want to try one more combination. I think that I see something happening. Let a = 2 and b = 7.
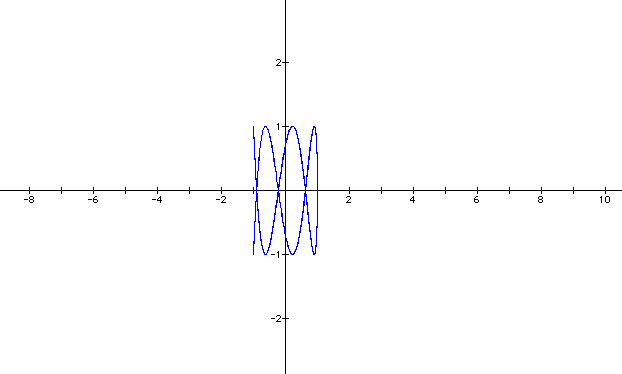
I noticed that whenever b was an odd number, the graph was open at one end. Whenever b was an even number, the graph was enclosed. Look at the graphs carefully. Do you see any other similarities?