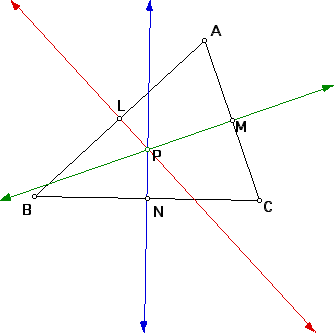
This assignment originated from assignment 8, EMAT 6680. Here we are to examine a triangle ABC, its circumcircle, and angles within the circle.
INSTRUCTIONS: The internal angle bisectors of triangle ABC are extended to meet the circumcircle at points L, M, and N, respectively. Find the angles of triangle LMN in terms of the angles A, B, and C.
First we need to construct the triangle ABC and its circumcenter. Remember, we construct the circumcenter using the perpendicular bisectors of each side of the triangle. The point of intersection of the perpendicular bisectors is the circumcenter, point P. So our graph would be

Now we need the circumcircle. This is constructed with P as the center and PA, PC, and PB as radii.
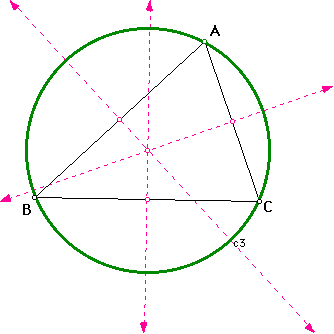
Now we need to construct the angle bisector for each vertex.
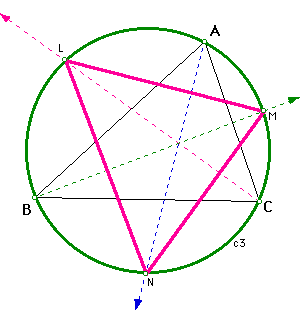
Remember that we are to find the angles of LMN in terms of ABC's angles. Below shows the graph with the angles labeled, the circumcircle, and triangles ABC and LMN.
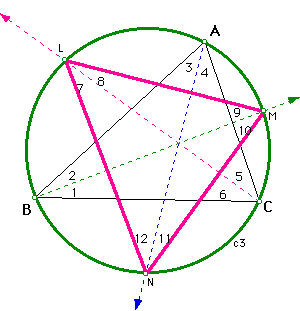
Angle 7 = angle 4 because they subtend the same arc of our circle. Angle 8 = angle 1; angle 2 = angle 11; angle 3 = angle 10; angle 6 = angle 9; angle 5 = angle 12, by the same reasoning.
Angle A = angle 10 + angle 7.
Angle B = angle 8 + angle 11.
Angle C = angle 12 + angle 9.
Angle L = angle 7 + angle 8.
Angle M = angle 9 + angle 10.
Angle N = angle 11 + angle 12.
Therefore, angle L = 1/2 A + 1/2 B; angle M = 1/2 C + 1/2 A; and angle N = 1/2 C + 1/2 B.