Triangles have various centers with their own characteristics. I have chosen to examine the orthocenter and its particular characteristics. The orthocenter, usually denoted by the letter H, is the point of intersection of the triangle's three altitudes, one for each side. What is an altitude? An altitude is the line segment from a vertex drawn perpendicularly to its opposite side. Let's look at an arbitrary triangle with its altitudes.
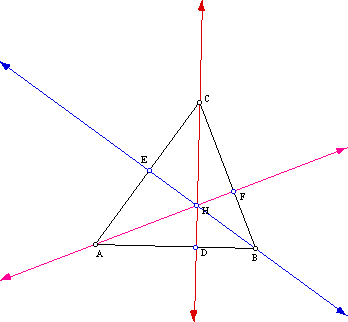
The point H is the orthocenter, while points D, F, and E are the "feet" of the altitudes. Does H always stay confined to the triangle's perimeter? Let's see.
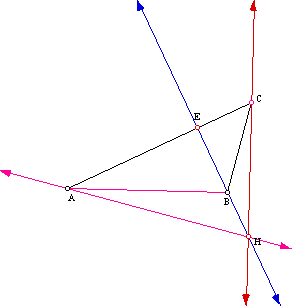
No, the orthocenter is not necessarily confined to the sides of the triangle. Note in the above graph that the feet of two altitudes, points D and F, have become one with the orthocenter. What will happen if the orthocenter is moved to one of the triangle's vertices? What will our graph look like if the orthocenter is located at vertex B?
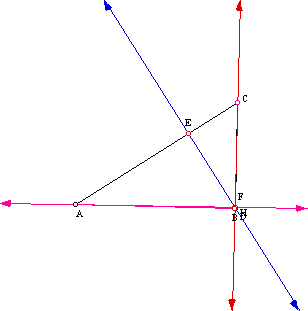
The orthocenter is combined with the points D and F. So we see that the orthocenter can be located within, without, and on the sides of a triangle. What determines whether or not the center is located inside or outside the triangle? Let's look at an acute triangle (one with all acute angles), a right triangle (one with a right angle), and an obtuse triangle (one with an obtuse angle).

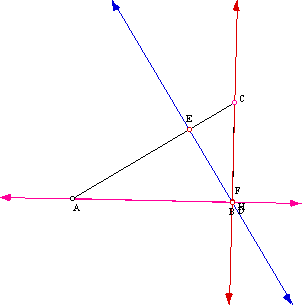
Examining the three graphs shows us that the orthocenter remains inside an acute triangle, lies on the triangle's side in a right triangle, and lies outside an obtuse triangle.