Consider the following exploration using Geometer's Sketchpad:

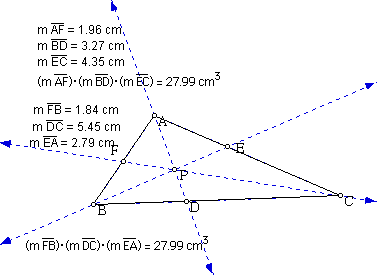
Consider any triangle ABC and select a point P inside the triangle. Draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. If we explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P, we will come to the conclusion that the product of the two are equivalent or the ratio of (AF)(BD)(EC)/(FB)(DC)(EA) = 1. The following GSP sketch shows one example of this.

In order to prove the conjecture that the ratio (AF)(BD)(EC) / (FB)(DC)(EA) = 1, we will need to construct parallel lines to CP through points A and B.

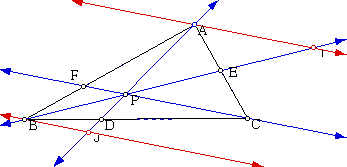
Once we do this, we have triangle PBF similar to triangle IBA by Angle-Angle similarity. We also have triangle PAF similar to triangle JAB by Angle - Angle similarity. From this, we have the following ratios

and .

Also, triangles AEI and CEP are similar by Angle-Angle similarity (vertical angles and alternate interior angles). Likewise, triangles BDJ and CDP are similar (vertical angles and alternate interior angles). From these triangles being similar and the fact that corresponding parts of similar triangles are similar, we get the following ratios:

and .

From and , we get .

.

By working on the left side of the equation, we get the left side is equal to 1.

Thus, we have , which is what we wanted to prove.

We can generalize the result using lines rather than segments to construct ABC so that point P can be outside the triangle. One sketch follows that shows this.

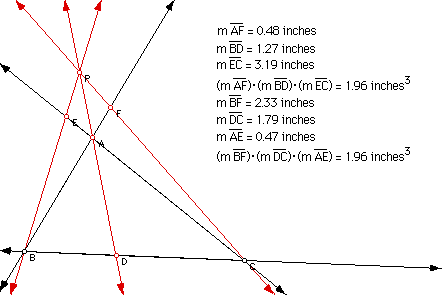
The product of (AF)(BD)(EC) is still equivalent to the product (BF)(DC)(AE).

By experimenting with Geometer's Sketchpad, we can conclude that the ratio of the areas of triangle ABC and DEF is always greater than or equal to 4. One example follows. Click here to try for yourself.

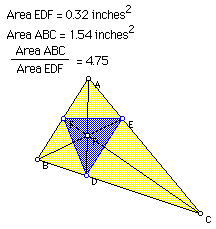
The ratio of the areas of triangle ABC and DEF will be equal to 4 when the areas of triangle AEF, BDF, CDE, and DEF are all equal. This will occur when E is the midpoint of AC, D is the midpoint of BC, and F is the midpoint of AB -- and point P will be the centroid of triangle ABC. With point P any other point, the ratio of the areas of ABC and DEF will be greater than 4.

Return to April's Home Page