Parametric Curves

April Kennedy

A parametric curve in the plane is a pair of functions

where the two continuous functions define ordered pairs (x,y). The two equations are usually called the parametric equations of a curve.

The most simple case involving sines and cosines would be the parametric curve

.

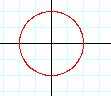
This graph is the one of the well known unit circle. The center of this circle is at (0,0). We will take a look at this graph and then how changing some values within the equation changes the graph.

What about the case where

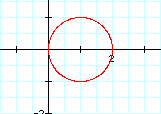
x = cos(t) + a , y = sin(t) + b OR x = cos(t) - a , y = sin (t) - b for the same t as above and different a's

.

x= cos(t) +1

y= sin (t)

 The center of this circle is at (1,0) and the radius is 1.

 

Let's look at a few more cases:

 x = cos (t) + 2

y = sin (t) + 4

 x = cos (t ) - 2

y = sin (t) - 2

x = cos ( t) + 4

y = sin (t) - 1

center: (2,4) center (-2, -2) center (4,-1)

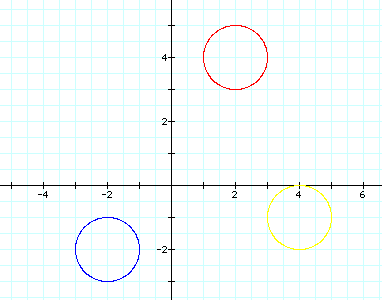
When 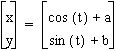, The graph is a circle with center at (a, b) and radius 1.

Let's look at the case when .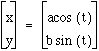

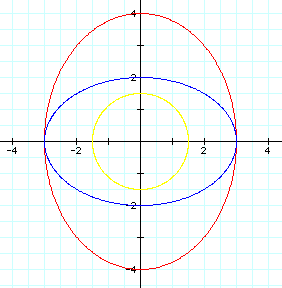
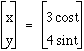Red curve = , Blue Curve = 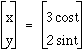, and

Yellow Curve = .

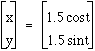When a and b change in the equation, we get some unique graphs. When a< b, the curve is an ellipse with the minor axis on the x-axis. This is the case in the red ellipse. When a = b, the curve is a circle. The major and minor axes have the same length. This is the case in the yellow curve. When a>b, the curve is an ellipse with the minor axis on the y-axis and the major axis on the x-axis. This is the case in the blue ellipse. A and B tell us 1/2 the length of the major and minor axis.

More Explorations:

For some interesting graphs, go to a Graphing Calculator program and try graphing some equations such as

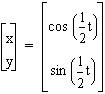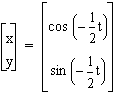, , or .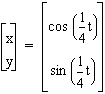

Which of these do you think would produce the following graph?

 

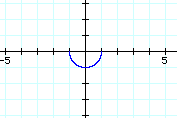
Return to April's home page