

After thinking about problems that many
high school classrooms spend much time on, the problem of how
the graph ![]() changes as a changes seemed to be a topic that much time is
spent on. We will look at how this graph changes for varying a'
s and how a student could easily understand
this concept using Graphing Calculator. For the graph
changes as a changes seemed to be a topic that much time is
spent on. We will look at how this graph changes for varying a'
s and how a student could easily understand
this concept using Graphing Calculator. For the graph ![]() where
a varies, there is always a common point on each
graph. For various a's, integer values or decimal values, the point
(0,0) will always lie on the graph. In fact, (0,0) is the vertex
of each graph.
where
a varies, there is always a common point on each
graph. For various a's, integer values or decimal values, the point
(0,0) will always lie on the graph. In fact, (0,0) is the vertex
of each graph. ![]() is a parabola extending to infinity,
either opening upward from the origin if a is positive or opening
downward from the origin if a is negative.
is a parabola extending to infinity,
either opening upward from the origin if a is positive or opening
downward from the origin if a is negative.
As the values of a increase
from 0 to infinity, the parabola contracts toward the positive
y-axis but never touches it. If the values of a decrease from
0 to negative infinity, the parabola contracts toward the x-axis
but never touches the x - axis. By looking at the graph below,
we can see the many ways that the graph changes as a
varies. The examples on my graph are
![]() (blue),
(blue),
![]() (purple),
(purple),
![]() (red) ,
(red) ,
![]() (green).
(green).
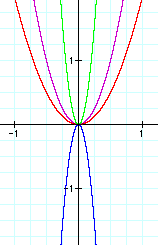
By looking at the graph, we can tell that larger a values make the graph move closer to the y-axis. Smaller a values move the graph away from the y-axis. This works for non-integers as well as integers.
An exercise like this is one that is predominant in high school classrooms. Having the students examine one graph and then overlay another graph on top of that one seems to be a useful practice. Once the student has several graphs on the same coordinate axis, he can tell how the value of a changes the shape of the curve.
More explorations:
What happens when we have y = x^2 +a and a varies?
What about x^2 -a?