Constructing a triangle and it's triangle of medians, one will find some very interesting discoveries. When I talk of a triangle of medians I am referring to a triangle with the three sides the lengths of the three medians in an original triangle. What kinds of relationships can we find between the two triangles? I have constructed some triangles and their triangle of medians using Geometer's Sketchpad so that I could observe some properties of these two triangles and compare certain attributes of these triangles. Comparing some of the different triangles, I realized that the triangles are not congruent, however they are similar. These two triangles do not have the same area, but the ratio of the area of the triangle of medians to the original triangle will always be 3:4.
I have chosen to look at three different types of triangles and see what results when we construct the triangle of medians. We will take a look at equilateral triangles, isosceles triangles, and right triangles.
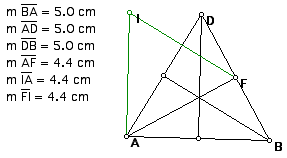
Given an equilateral triangle ABD with medians, I created a triangle of medians, AFI. By the measurements to the left of the triangle, we can see that the triangle of medians is also equilateral.
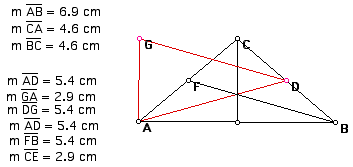
Given an isosceles triangle ABC, I have constructed it's triangle of medians ADG. Will this triangle of medians also be an isosceles triangle? By looking at the sketch below and the measurements to the left, we can see that triangle ADG is also an isosceles triangle since two of the sides of the triangle have the same measure.
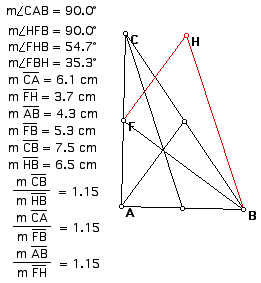
Let's look at case 1 of the right triangles. Take the right triangle ABC below and it's triangle of medians FBH. By taking the measurements of some of the angles, we can see that triangle FBH is not a right triangle. So, we can conclude that a right triangle does not always have a triangle of medians that is a right triangle. This does not mean that it cannot have a right triangle of medians, but it must be a special case. We will look at this case in case 2.
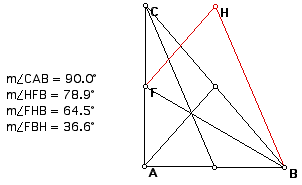
In the right triangle below, you will notice that the triangle of medians is also a right triangle with right angle HFB. What is special about this triangle that was not about the one above? If we look at the measurements to the left of the triangle, we will notice that the ratios between the sides of the original triangle and the sides of the triangle of medians are the same. This has to be the case in order for the triangle of medians to also be a right triangle. Why must this be the case?