

How are they related?
April Kennedy
I will examine the problem, construct any triangle ABC and the altitudes of each side, then examine the triangle formed by the points where the extended altitudes meet the circumcircle. We will then see how this triangle is related to the Orthic triangle (a description follows of what the orthic triangle is and how to construct it).
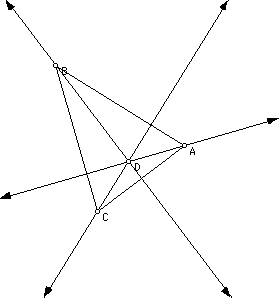
Let's first take a look at triangle ABC, the altitudes of the triangle, and the circumcircle of triangle ABC. If one remembers, the altitudes of the triangle are the lines from a vertex perpendicular to the opposite side. Looking at the picture below, you can see the altitudes and the point of intersection.
Let's go a step farther and look at the triangle formed by the points of intersection of the altitudes and the circumcircle. The circumcircle is formed by creating the perpendicular bisector of each side, finding the point of intersection (the circumcenter), and constructing a circle by center and point. In the sketch below, triangle QMO represents this triangle.
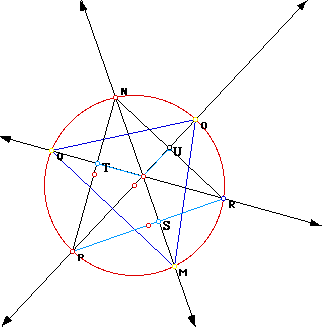
Let us now look at the orthic triangle and compare the two triangles. An ORTHIC triangle is formed by connecting the feet of the altitudes.
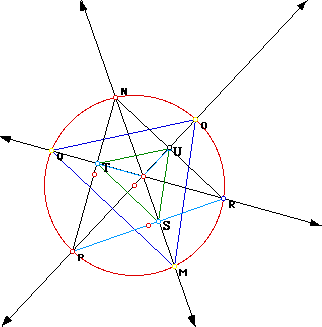
In the sketch above, TSU is the orthic triangle of triangle NPR. QMO (blue triangle) is the triangle formed by the points where the extended altitudes meet the circumcircle. Let's now explore some relationships. Triangle QMO is similar to triangle TSU, the orthic triangle because the meaure of the angles are the same and the sides have corresponding ratios. The ratio of the lengths of triangle QMO to TSU is 2:1. What about the areas? Do they have any relationship? In fact, they do. The area of the QMO is 4 times the area of the orthic triangle because the ratio is 2:1. Doing some algebra, we can see this quite easily. Let the area of TSU be A = 1/2 bh. Then, the area of QMO = 1/2 (2b) (2h). This is equivalent to A = 2bh which is 4 times 1/2bh.
Extensions:
1. Are there other relationsips between these two triangles?
2. Are there any relationships between the original triangle NPR and QMO or TSU?
Return to April's home page