

Anecdote about Napoleon Bonaparte (1769-1821)
Napoleon was known as an amateur mathematician. There is a historical anecdote about Napoleon who was emperor of the French:
It is known that Napoleon Bonaparte was a bit of a mathematician with a great interest in geometry. There is a story that, before he made himself ruler of the French, he engaged in a discussion with the great mathematicians Lagrange and Laplace until the latter told him, severely, "The last thing we want from you, general, is a lesson in geometry," Laplace became his chief military engineer.
What is Napoleon's Triangle?
Given any triangle, construct equilateral triangles on each side and find the center of each equilateral triangle. The triangle formed by these three centers is Napoleon's Triangle.
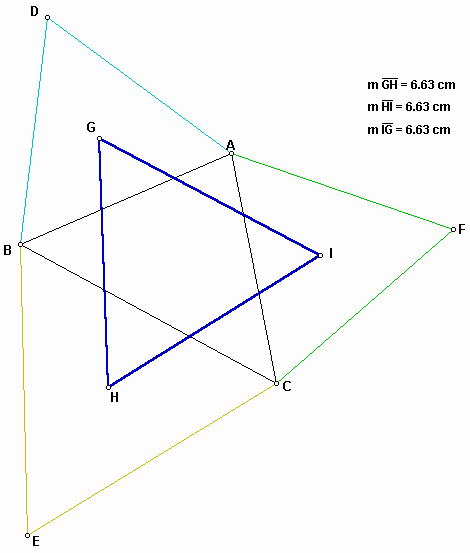
Napoleon's Theorem: If equilateral triangles are erected externally on the sides of any triangle, then their centers form an equilateral triangle.
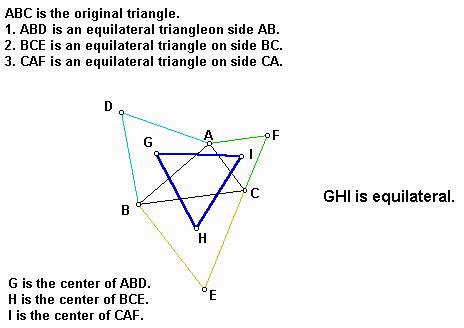
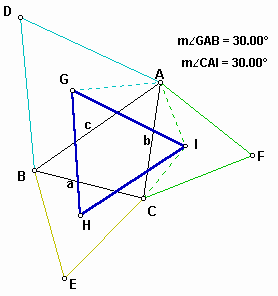
Indeed, the shape of the resulting triangle, that is equilateral triangle does not depend on the shape of the original triangle. In other words, no matter what shape the original triangle has, we get the equilateral triangle constructed by the centers of the three equilateral triangles which were obtained from the original one. In the figure 1, the triangle GHI is called as the outer Napoleon triangle of the triangle ABC.
When we construct the equilateral triangles on each side of a given triangle, there exist two equilateral triangles on each side.
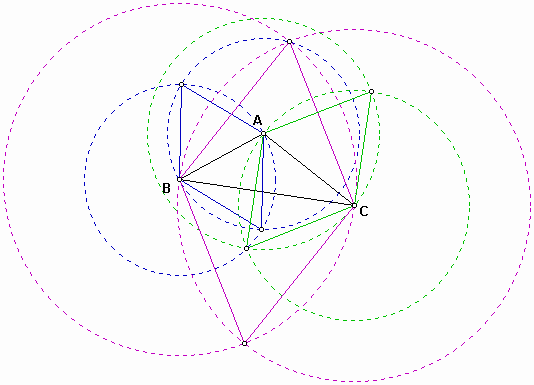
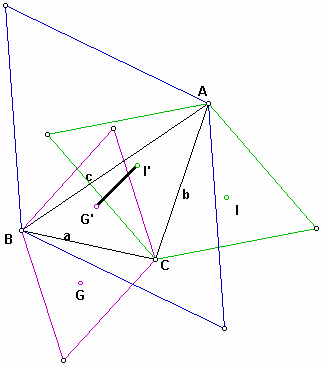
If equilateral triangles are erected internally on the sides of triangle ABC, as in the figure 2, their centers form the inner Napoleon triangle.
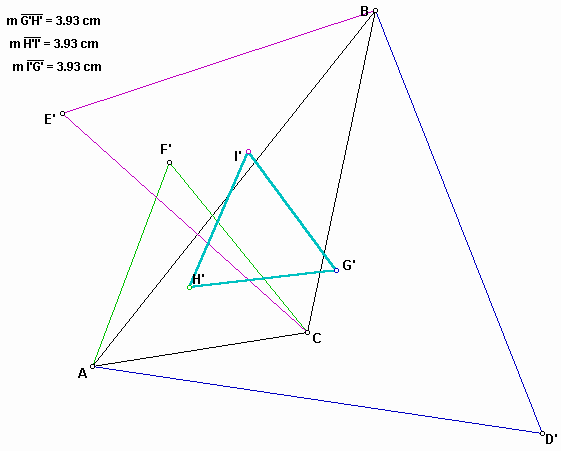
From the above, we can rewrite the Napoleon's theorem as follows:
1. The outer Napoleon triangle is equilateral.
2. The inner Napoleon triangle is equilateral.
Proof of Napoleon's theorem
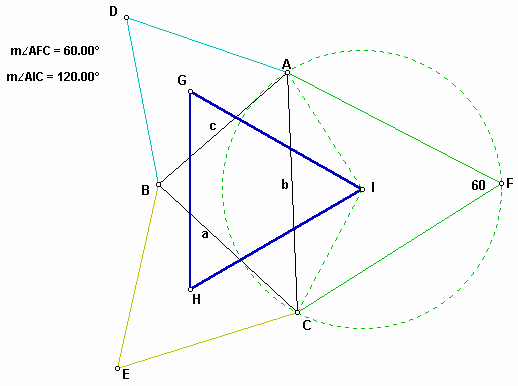
As you notice in the figure 4, AI is the circumradius of an equilateral triangle of side AC.
If we apply the second Cosine law in the following:
Since
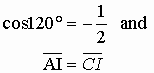 ,
,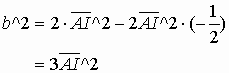
Now we have
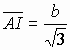
Similarly,
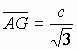
Obviously,
Thus,
Since G' and I' of the inner Napoleon triangle can be derived from G and I by reflection in the lines CA and AB, respectively, and
we get
If we subtract equation (2) from equation (1), we obtain:
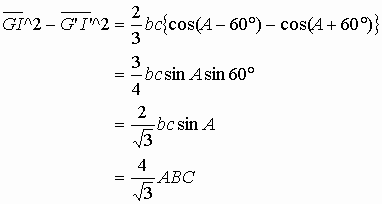
Likewise, we gain
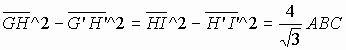
We already know that
and get
Another Proof using by Plane Tesselation
References
Coxter, H. S. M. & Greitzer, S. L. (1967). Geometry Revisited. New York: Random House, Inc.
http://www.mathworld.wolfram.com/NapoleonsTheorem.html
http://cedar.evansville.edu/~ck6/tcenters/class/napoleon.html