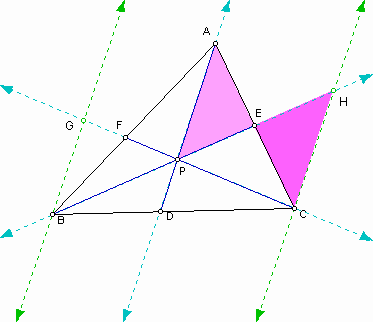
Part A.
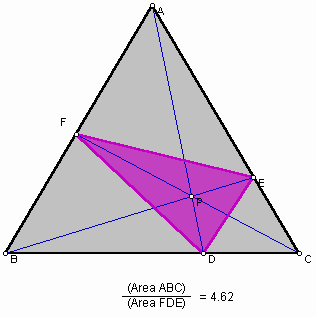
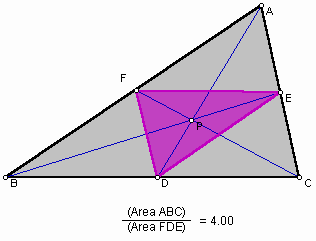
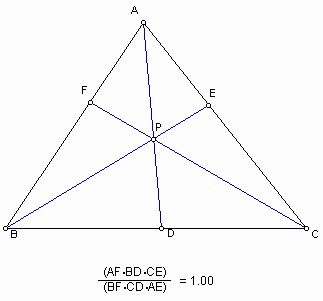
We have a triangle ABC and any point P in the triangle. Draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.
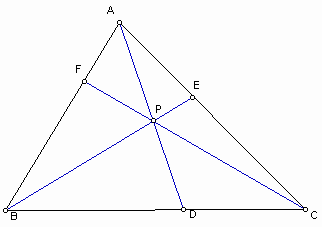
Through the exploration of various triangles and various location of P that is inside the given triangle, we can conjecture that (AF)(BD)(CE) is always equal to (BF)(CD)(AE).
To prove our conjecture, we need some parallel lines to line AD, which go through point B and C:
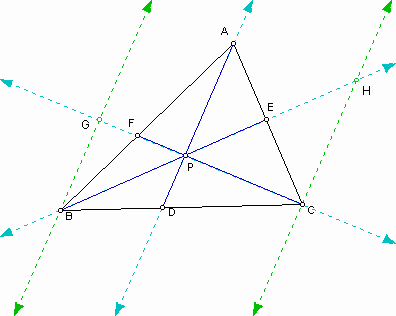
You can find similar triangles from the above figure.
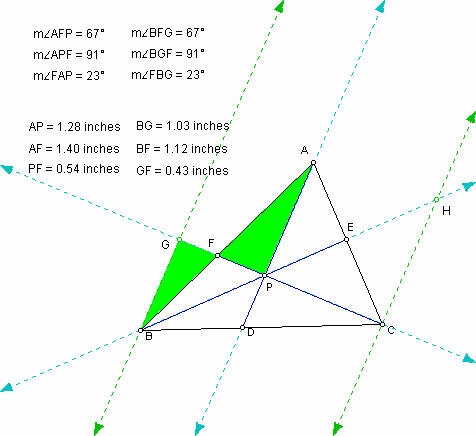
1. Triangle AFP is similar to triangle BFG because each corresponding angle is congruent. As a result, we have
2. Triangle BPD is similar to triangle BHC and we know
3. Triangle CPD is similar to triangle CGB and we get
4. Triangle AEP is similar to triangle CEH, which results in
From the results that we have got above explorations, we can get the following:
From the second and third ratio we can also have
Consequently, we can now get
Part B.
Consider the point P is outside the triangle. And in that case the ratio that we proved above, can the result, that we conjectured and finally proved above, be generalized?
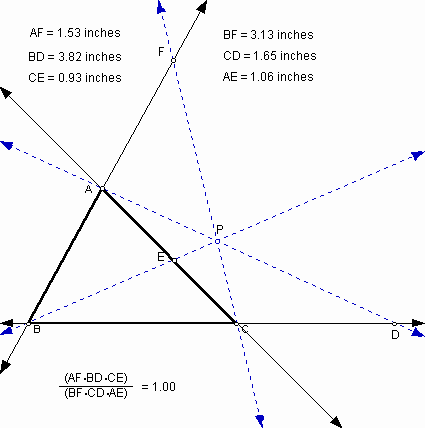
As you see above picture, the ratio still holds if the point P is outside the triangle. Go to the GSP file to explore by changing the location of P.
Part 3.
When P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. We are going to see when it is equal to 4. You can see that in GSP file.