Orthocenters
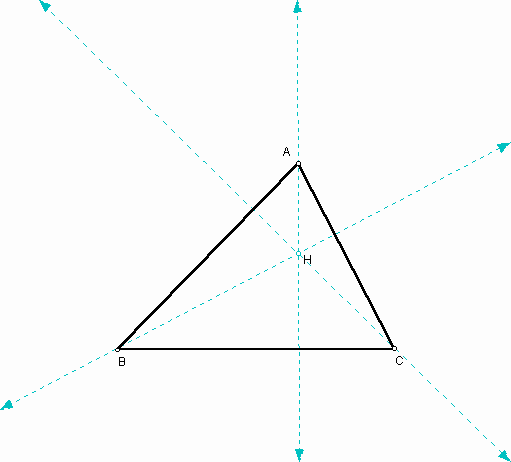
There is a triangle. We can construct orthocenter (H) of the triangle:
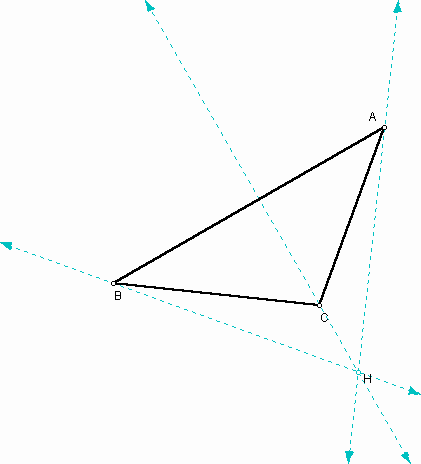
We can construct orthocenters of triangles HBC, HAB, and HAC:
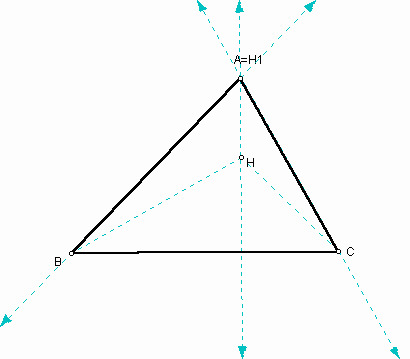
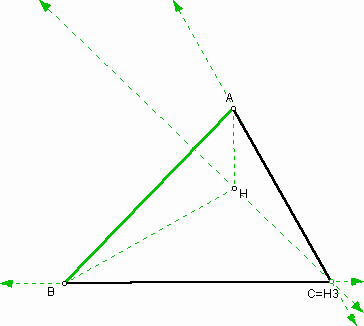
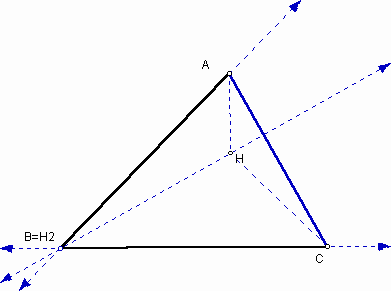
As you observe the orthocenters of trianles HBC, HAB, and HAC are the vertices of the given triangle ABC, respectively. The orthocenter H is constructed by the perpendicular lines from the vertices and as a result, new sides of new triangle of HBC, HAB, and HAC are a part of the perpendicular lines. Also you can see that it always keeps no matter where the orthocenter H is in the following GSP file.
Circumcircles of the triangles
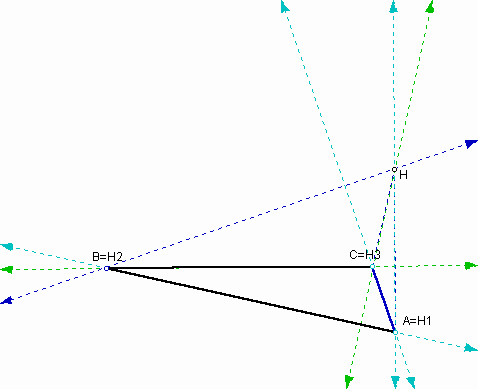
We now are going to construct circumcircles of each triangle. In order to do that we need to find the circumcenters of the triangles. First, we can get the circumcenter C of the given triangle ABC:
You might notice that all lines which are required to get the circumcenter of triangle ABC are paralled to perpendiculare lines in the above picture. Also this property doesn't change even if the location of circumcircle moves around in the plane.

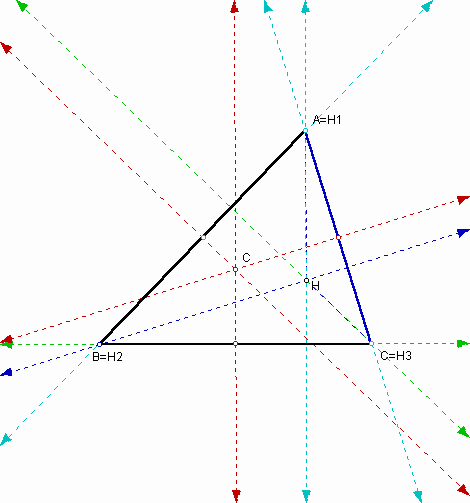
The circumcircles of triangles ABC, HBC, HAB, and HAC are shown in the following (C, C1, C2, and C3 represent both center and circumcircle of triangles, respectively):
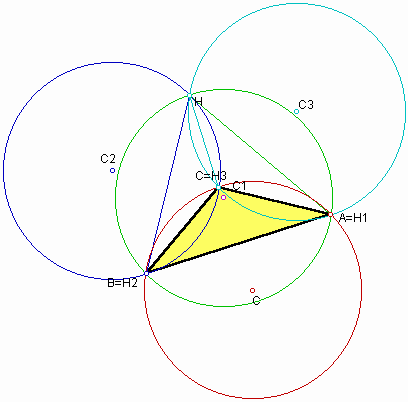
When the center C1 coincides with C, the circumcircle C1 also coincides with the circumcircle C. And at that time triangle ABC is right triangle. Likewise, you can observe the same phenomena when the center C2 and C3 are at the center C. In addition, if any two circumceters meet, the orthocenter H of triangle ABC coincides with one of the orthocenters of HBC, HAB, and HAC.
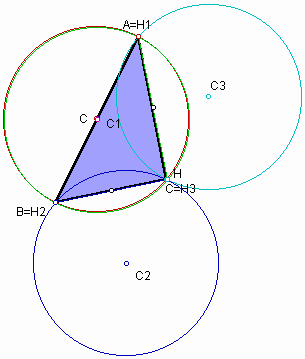
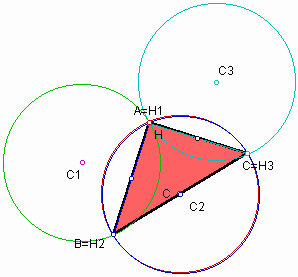
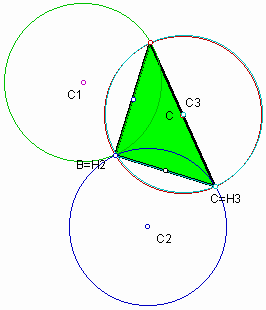
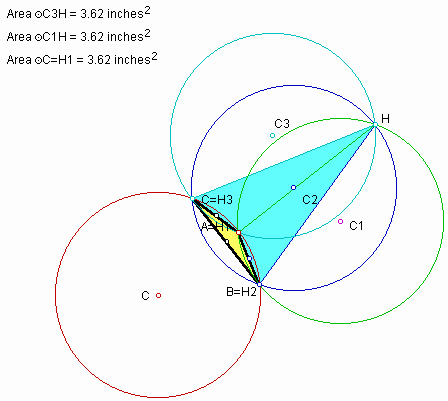
The areas of the circumcircles
From the above pictures we can conjecture all circumcircles have the same areas. You can explore it according to the various of triangles and the location orthocenter H by draging the vertices A, B, and C in the GSP file.
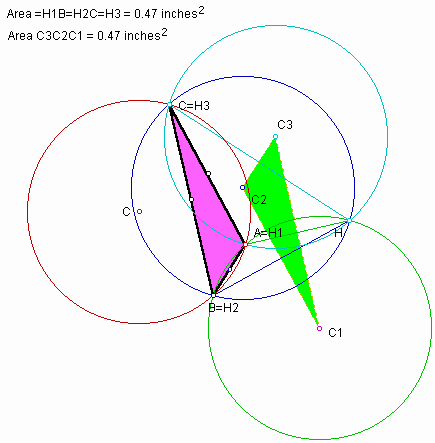
Areas of traiangles
Comparing the area of triangle ABC and the area of triangle C1C2C3, we can see the fact that they are always equal. If you go to GSP file , you are able to explore such property by yourself.