

Ceva's Theorem
was discovered by and named for Giovanni
Ceva. Ceva's Theorem states: Given any triangle ABC,
the segments from A, B, and C to the opposite sides of the triangle
are concurrent precisely when the product of the ratios of the
pairs of segments formed on each side of the triangle is equal
to 1. The theorem is easier to understand if you look at the following
picture (Figure 1). AB, BC, and CA are concurrent if AF/FB*BD/DC*CE/EA=1.
The converse is also true. If AF/FB*BD/DC*CE/EA=1 then AB, BC,
and CA are concurrent.
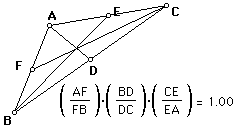
Because of Ceva's Theorem, the lines joining a vertex of a triangle with a point on the opposite side (AB, BC, and CA) are known as Cevians (Bogmolny). Although Figure 1 only shows Cevians that lie inside the triangle, Ceva's theorem is still true when the Cevians do not all lie in the interior of the triangle. While many people have never heard of Ceva's theorem, most people have seen examples of Cevians somewhere in geometry. For example, the medians of a triangle, the angle bisectors of a triangle, and the altitudes of a triangle are all examples of Cevians.
There are several proofs of Ceva's Theorem,
but the usual proof involves
extending segments of the triangle and considering the similar
triangles that are formed (Bogomolny).
A second proof of Ceva's
Theorem does not involve similar triangles. Instead, it uses the
theorem that the areas of triangles with equal altitudes are proportional
to the bases of the triangles (Coxeter, 4).
Ceva's Theorem
also gives rise to several Corollaries. The first three Corollaries
that arise from Ceva's Theorem have already been mentioned.
They are:
Corollary 1: The medians of a triangle intersect at a single point
(proof). The point of intersection
of the medians of a triangle is referred to as the centroid.
Corollary 2: In a triangle, the angle bisectors intersect at a
single point (proof). The intersection
point of the angle bisectors of a triangle is referred to as the
incenter of the triangle.
Corollary 3: In a triangle, the altitudes intersect at a single
point (proof). The intersection
point of the altitudes of a triangle is known as the orthocenter
of the triangle.
Another interesting Corollary to Ceva's Theorem involves the Gergonne point. The Corollary states: Let D, E, and F be the points where the inscribed circle touches the sides of the triangle ABC. Then the lines AD, BE, and CF intersect at one point. (essay 2: Gergonne Point)
The last Corollary to Ceva's theorem that we will mention involves the isotomic conjugates of concurrent Cevians. The Corollary states: For three concurrent Cevians AD, BE, and CF, if the point D, E, and F are reflected in the midpoints of the corresponding sides, the resulting three lines form another triplet of concurrent Cevians. The resulting Cevians are referred to as isotomic conjugates of the original Cevians. The proof of this theorem is rather simple because the ratios are simply inverted. So the product of the inverted ratios is still 1.
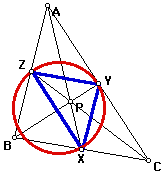
Within triangle ABC with Cevians AX, BY, and CZ, there is the Cevian triangle and the Cevian circle. The Cevian triangle is the triangle with vertices at the endpoints of the Cevians through P (triangle XYZ). The Cevian circle is the circumscribed circle of the Cevian triangle. In other words it is the circle that passes through all three vertices of the Cevian triangle. The Cevian triangle and the Cevian circle are shown for triangle ABC in figure 7 (Weisstein).
Besides Ceva's Theorem, Giovanni Ceva is also credited with rediscovering and publishing Menelaus' Theorem (JOC). Menelaus' Theorem is very closely related to Ceva's Theorem. Both Ceva's Theorem and Menelaus' Theorem use the statement BD/CD*CE/AE*AF/BF=1. Ceva's Theorem states that if the three Cevians of a triangle are concurrent then the previous statement holds. On the other hand, Menelaus' Theorem states that if points D, E, and F on the sides BC, CA, and AB of triangle ABC are collinear, then the previous statement holds. Some references state Menelaus' Theorem in the following way: given any line that transverses (crosses) the three sides of a triangle (one of them will have to be extended), six segments are cut off on the sides. The product of three non-adjacent segments is equal to the product of the other three segments (Wilson). Both statements of Menelaus' Theorem are equivalent. So Menelaus' Theorem provides a criterion for collinearity, while Ceva's Theorem provides a criterion for concurrence (Coxeter, 67).
Like Ceva's Theorem, the proof
of Menelaus' Theorem also involves similar triangles (No
Author). Another proof of
Menelaus' Theorem involves using different similar triangles
(Wilson). The converse of Menelaus' Theorem is also true.
If BD/CD*CE/AE*AF/BF=1 then D, E, and F are collinear.
A famous theorem that depends on Menelaus' Theorem is Desargues' Theorem. Desargues' Theorem states: Let ABC and A'B'C' be two triangles. If the lines AA', BB', and CC' concur in one point, then the intersection point of AB and A'B', the intersection point of BC and B'C', and the intersection point of AC and A'C' are collinear. The converse of this theorem is also true. If the three mentioned intersection points are collinear, then AA', BB', and CC' concur in one point (Floor).
Both Ceva's theorem and Menelaus' theorem have been important contributions to the study of geometry. Ceva's Theorem is used in the proofs of many well-known theorems including the theorem of Napolean's point, the theorem of Fermat's point, and the theorem of the Nagel point. Because Ceva's Theorem and Menelaus' Theorem deal with ideas that are so basic to the study of geometry, concurrence and collinearity, it is impossible to overlook them. However, many high school and college geometry courses do not mention Ceva's Theorem or Menelaus' Theorem. But none the less, the principles behind both of the theorems are used and studied often in any geometry class.
Return to Essay 2: Gergonne Point