

Napoleon's Theorem goes as follows: Given any arbitrary triangle ABC, construct equilateral triangles on the exterior sides of triangle ABC. The segments connecting the centroids of the equilateral triangles form an equilateral triangle.
Let's explore this theorem.
Construct an equilateral triangle and see if Napoleon's triangle is equilateral.
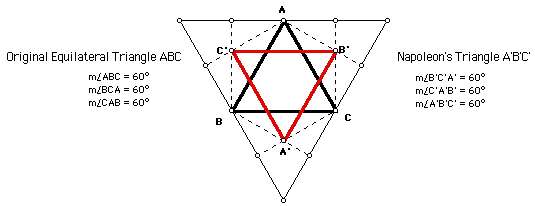
We can see from this construction, that when given an equilateral triangle, the resulting Napoleon triangle is also equilateral.
Construct an isosceles triangle.
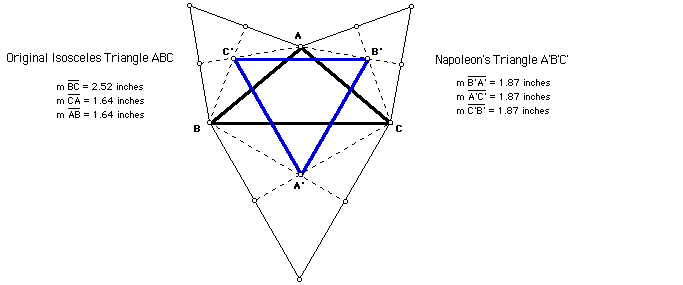
Again, we see that with an isosceles triangle, Napoleon's triangle is still equilateral.
Now, let's construct a right triangle.
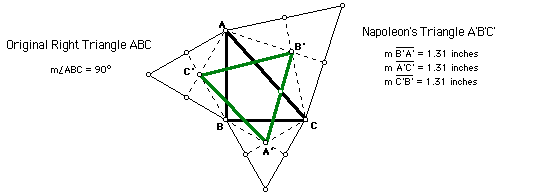
Still, even with a right triangle, Napoelon's triangle is equilateral.
Now, we will prove that for any given triangle ABC, Napoleon's triangle is equilateral. We will use the following diagram:
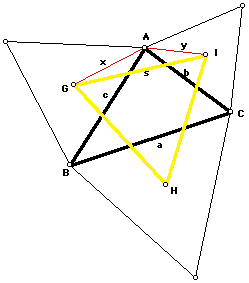
A represents vertex A and it's corresponding angle. a denotes the length of BC, c denotes the length of AB, and b denotes the length of AC. G, I, and H are the centroids of the equilateral triangles. x is the length of segment AG and y is the length of segment AI. s is the length of GI.
Proof:
Since angle IAC=angle GAB=30 degrees, let's apply the Law of Cosines: s^2 = y^2 + x^2 - 2yx*cos(A + 60 degrees).
Since the centroid of a triangle lies along each median 2/3 of the distance from the vertex to the midpoint of the opposite side, then:
Substituting these values, we have: 3*s^2 = b^2 + c^2 - 2bc*cos(A + 60 degrees). Let's expand the cosine of the sum, and recall that cos(60 degrees) = 1/2 and sin(60 degrees) = sqrt(3)/2. So we have: cos(A + 60 degrees) = cos(A)/2 - sin(A)*sqrt(3)/2.
Substituting, we have 3*s^2 = b^2 + c^2 - bc*cos(A) + sqrt(3)*bc*sin(A).
Now apply the Law of Cosines to triangle ABC: a^2 = b^2 + c^2 -2bc*cos(A).
Recall, as in the derivation of the Law of Sines, that 2*area of triangle ABC = bc*sin(A)
Substituting, we have: 3*s^2 = (1/2) (a^2 + b^2 + c^2) + 2*sqrt(3)*area of triangle ABC.
Since the above equation is symmetrical in a, b, and c, it follows that the triangle (Napoleon's triangle) connecting the three centroids is equilateral. QED.