Triangle Ratio Investigation/Final Project

This assignmnet involves beginning with any arbitrary triangle ABC. We select a point P inside the triangle and construct lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. This is shown in the diagram below.
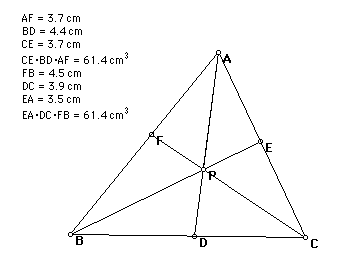
In this particular triangle,
(AF)(BD)(EC) = (FB)(DC)(EA). This is true for various other triangles
and various other locations of P. A conjecture can be made that
for all triangles ABC with P, D, E, and F as described above,
(AF)(BD)(EC) = (FB)(DC)(EA).
Click Here to see
a proof of this conjecture.
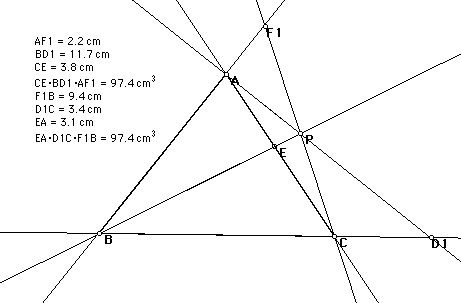
The
above conjecture is true even when point P is outside the triangle.
Click Here to explore the picture below using GSP.
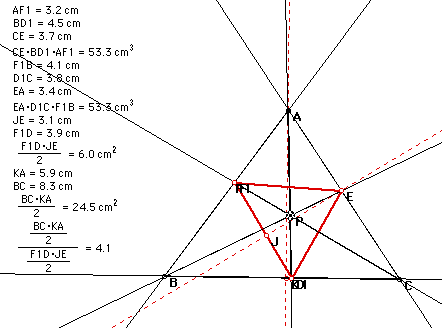
When P is located inside triangle
ABC, the ratio of the areas of triangle ABC and DEF is always
greater than or equal to 4.
Click Here to explore this conjecture.
Click Here to see when this ratio is equal to four.