

An equation of a line can be written in several different forms. It can be written in y-intercept form, point-slope form, and parametric form. The first scenario that will be investigated in this write-up is how a parametric equation for a line can be determined when the slope of the line and a point on that line is given. Let's look at an example:
Write parametric equations of a line through (7,5) with slope of 3.
The Point-Slope form gives us an equation that reads y-5 = 3(x-7). If we set this equation equal to t, we get t = y-5 and t = 3x-21 which gives us y = t +5 and x = t/3 + 7. A graph of this equation is shown below.
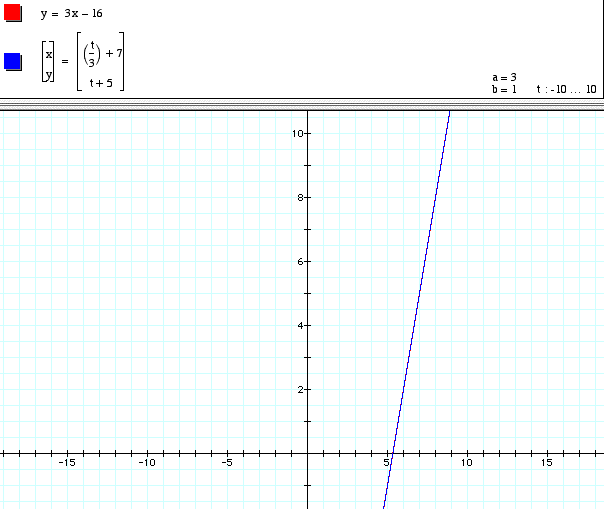
If the point and slope of a line are known, parametric equation for this line can be determined. If the slope is given as m and a point (a, b) is given, the parametric equation can be given as:
x = (1/m) t + a and y = t + b
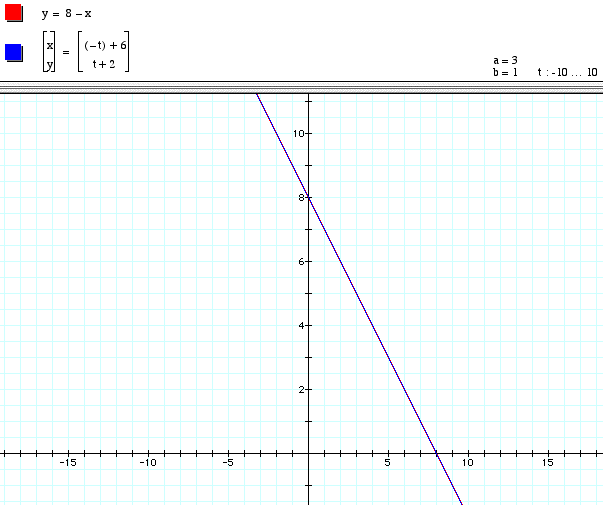
Another example of this generalization is given below:
The next step is to determine the Point-Slope or y-intercept form of the line given the parametric equation. We will start by graphing x = t + 1 and y = 2t -1, to get idea of what this equation looks like.
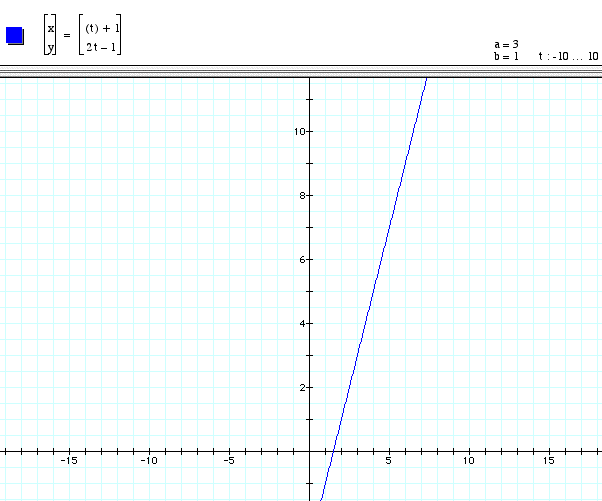
We can use algebra to solve for t on
both sides of the equation, giving us t
= x -1 and t
= y/2 + 1/2. When we set these equal
to each other, we get x -1 = y/2
+ 1/2 or y
= 2x-3 or y
+1 = 2( x -1). Therefore, if the
parametric equation is given as x
= t + a and
y = mt + b, then the Slope-Intercept
equation is given by y -b = m ( x
-a).
Looking back, it can be seen that in the first example, the slope was given by the inverse of the t-coefficient in x, but in the second equation, it was given by the t-coefficient in y. How can this be explained?
Click Here to see the answer
Return