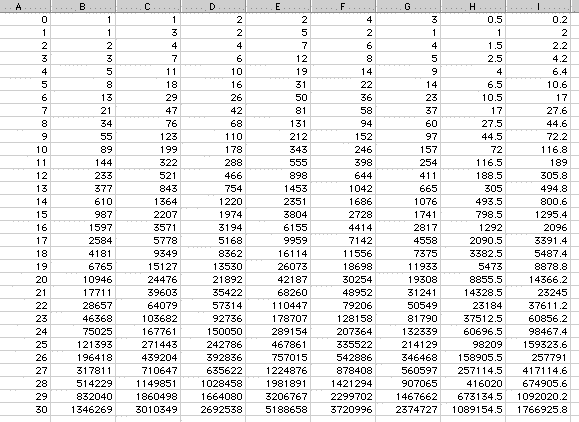
The Fibonnaci Sequence is generated by starting with the first two terms: F (0) = 1 and F (1) = 1. Each additional number in the sequence is given by F (x) = F (x-1) + F (x-2). In the Microsoft Excell Spreadsheet below, column A represents the value of x and column b represents the value in the sequence. Note the the increase is not a linear increase and almost appears to be an exponential increase. Column C displays the ratio of a value to the value before it, and approaches a limit at about 1.61803399. Column D displays the ratios of the C values, and reaches a limit of one because as column C reaches a limit, the preceeding term is equal to the following term. If the two terms are equal, their ratio is always one. The subsequent ratios could be explored, but their limits would always be one.
1.61803399 is an interesting limit because this ratio is also known as the Golden Ratio. It was the ratio used by Greek Geometers as they created the "Golden Rectangle", which is said to be the rectangle with the most pleasing porportions. Credit cards are often construction with this ratio of length to width. This ratio is also found in nature and human anatomy. It is the ratio of a person's total heighth to the heighth of the person's belly button. It is the ratio of a person's finger length to his/her knuckle length. It also found in flowers and has an infinite number of applications in science as well as math.
Column E represents the ratio of one term to the term following it, and the limit as x approaches infinity for this sequence is 0.61803399. This is interesting because it is exactly one less than limit when ratios were taken the opposite way. This is an interesting phenomena of this sequence. If column F is observed, it can be seen that the ratio of every second term appproaches zero in this instance as well. This occurs for the same reason it occurred in column D.
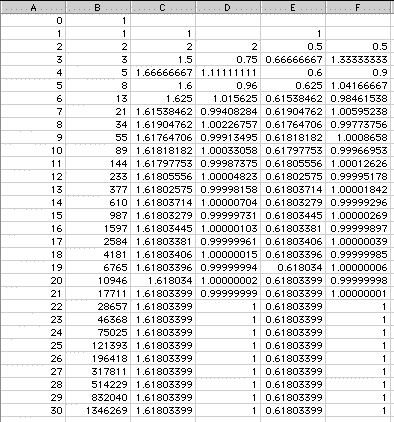
The Lucas Sequence is generated in much the same way as the Fibonnaci Sequence. The difference between the two sequences is that the Lucas Sequence starts with F (0)=1 and F(1)=3. This sequence follows much the same patterns as the Fibonnaci Sequence, as can be seen below. It appraches the same limits as the Fibonnaci Sequence, and in the same number as steps. F(30) is a sven-digit number for both sequences.
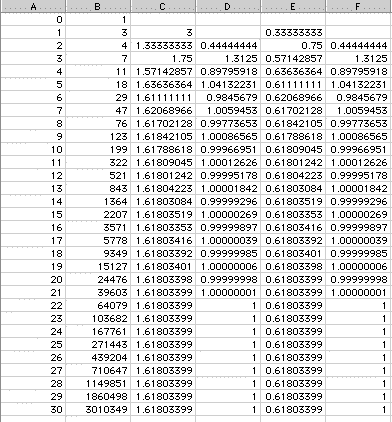
What do other sequences generated similarly to the Fibonnaci Sequence look like? The Spreadsheet below demonstrates different beginning numbers compared to the original Fibonnaci Sequence shown in column B. The 30th term for all these sequences is a seven-digit number and all appeaar to follow the same rapid increase trend of the fibonnaci sequence. Each of these sequences also hass the same ratio of the limit of successive terms.