

The Fermat Point (P) is the point at which the sum of the distances between P and each vertex of a triangle is minimized. This point can be constructed by creating an equilateral triangle on each of the sides of the original triangle and connecting opposite vertices as shown below:
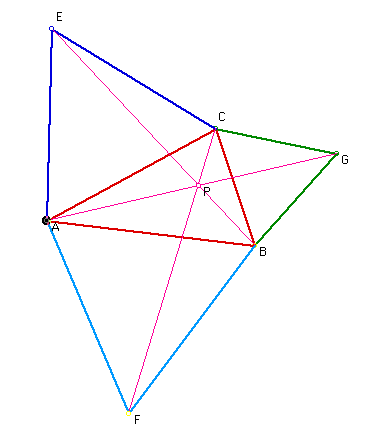
This point is also known as
the First Isogonic Center. (Isogonic means "equal angles").
It is called this because m(<BPC) = m(<CPB) = m(<APB).
These angles must add up to 360 degrees so each one must be equal
to 120 degrees.
What happens when triangle ABC contains
an angle of 120 degrees or larger?
Click Here to see a simplified
proof of the Fermat Point
Return