The object of this assignment is to examine the behavior of a chosen equation using Graphing Calculator software. I have chosen the equation below. Because I found it to have the most interesting behavior of the ten suggested equations.

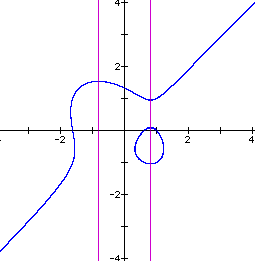
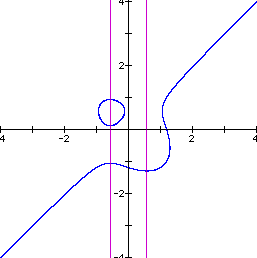
The graph of the equation appears below.

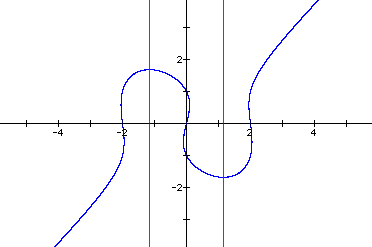
Setting the 4 in the original equation to 1 gives the graph below.

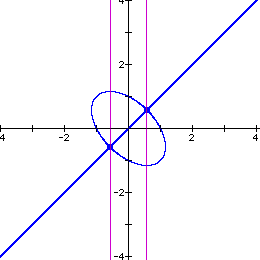
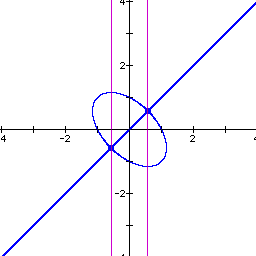
The graph now appears to be an ellipse bisected by the line y = x. Some experimentation determined that the equation is the product of the ellipse and the equation y = x. The pink lines in the graphs intersect the critical points of the equation determined by setting the derivative of the equation to zero.

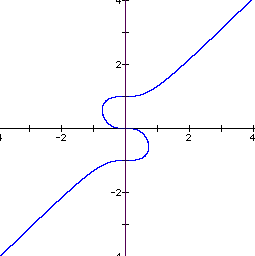
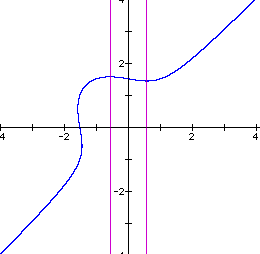
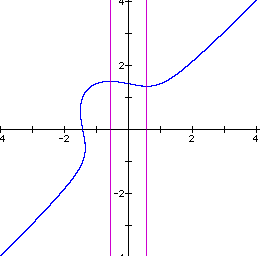
In order to study the bahavior of this equation, I replaced the 4 on the LHS of the original equation with n and let n vary from 0 to 2 and watched the results. The next 5 graphs show the behavior varying n from 0 to 2 in steps of 0.5.

n=0

n=0..5

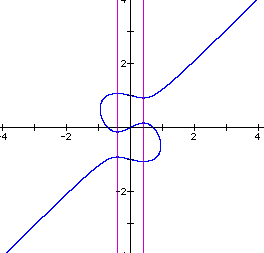
n=1

n=1.5

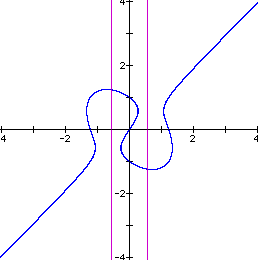
n=2

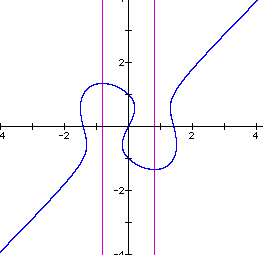
Notice that the axes through the critical points begin at x = 0 and gradually move outward as n increases. When n = 1, the axes intersect the intersection of the line and the ellipse as well as going through the critical points.

Another question that arises is, what if a constant is added or subtracted from the RHS? First, add 1 to the RHS and observe the new behavior by varying n over an appropriate interval. Now when n = 1 we have a different graph. The ellipse is gone. (see below) As a matter of fact, the equation now has only one real root. Where did the other two roots go?

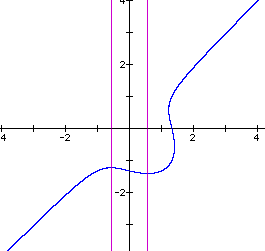
Let us see the effect of changing the value of n. First let n = 2. We get the graph below.

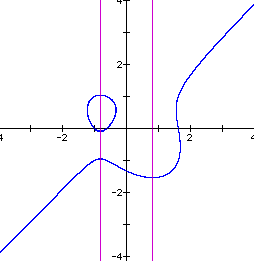
Now there is a small irregularly shaped closed curve appearing mostly in the second quadrant. We also now have three real roots. An interesting question now would be, at what value of n do the two real roots associated with the closed curve become imaginary roots?

Some trial and error will get us to the value n = 1.89. Look at the graph below for n = 1.89.

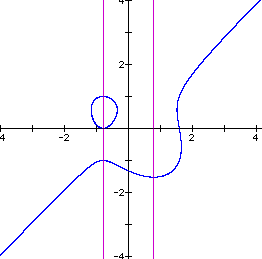
What happens to the graph as we let n increase beyond 1.9? At n = 2.35 the we get the graph below.

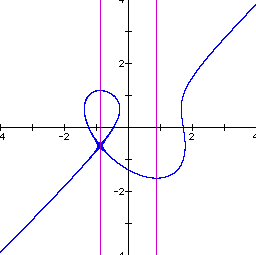
Notice that the closed curve now seems to be a loop in the graph of the equation with the intersection just below a critical point. As we increase n further this loop breaks and we obtain one continuos curve for the graph. See below for n=3.

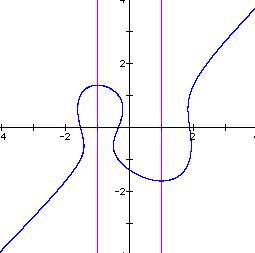
There is a similar behavior if we subtract one from the RHS of the equation. The graph below illustrates this. Here we have subtracted one from the RHS and set n to 1.

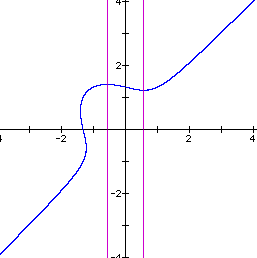
This graph is a reflection of the previous graph where we added one to the RHS about the origin. To better show this, let n = 2 and regraph the equation. See below.

Let us fix n at 1 and vary the adder to the RHS of the equation and see what effect will occur. The following graphs illustrate what happens as we vary the RHS adder from -2 to 2 in steps of 0.5.

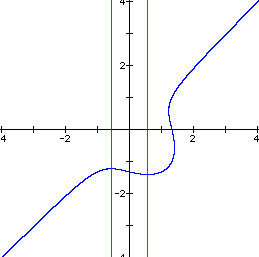
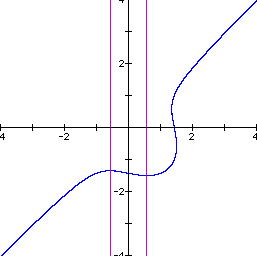
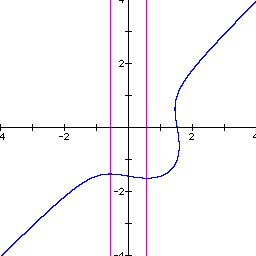
Most of the behavior of this equation is caused by the composite nature of the equation. We have an ellipse multiplied by a straight line. Since the equation is not a function, we are not guaranteed that we will always have a continuous curve for all values of the constants in the equation. In fact, for this equation, as we have shown, there are sometimes two distinct curves that are a part of the graph. Further investigation might include the product of a hyperbola and a line or the product of a parabola and a line. Or maybe even the product of two conics.