It has now become a rather standard exercise, with availble technology, to construct graphs to consider the equation

and to overlay several graphs of

for different values of a, b, or c as the other two are held constant. From these graphs discussion of the patterns for the roots of

can be followed. For example, if we set

for b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the following picture is obtained.

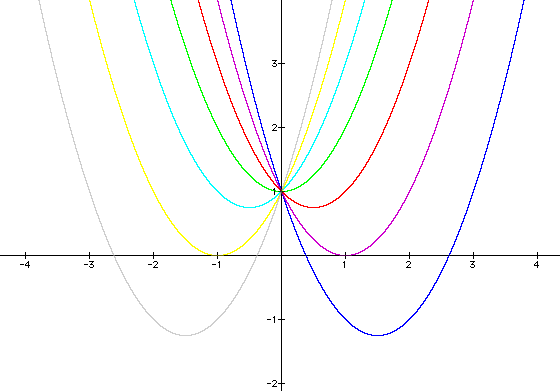
We can discuss the "movement" of a parabola as b is changed. The parabola always passes through the same point on the y-axis ( the point
(0,1) with this equation). For b < -2 the parabola will intersect the x-axis in two points with positive x values (i.e. the original equation will
have two real roots, both positive). For b = -2, the parabola is tangent to the x-axis and so the original equation has one real and positive root
at the point of tangency. For -2 < b < 2, the parabola does not intersect the x-axis -- the original equation has no real roots. Similarly for b =
2 the parabola is tangent to the x-axis (one real negative root) and for b > 2, the parabola intersets the x-axis twice to show two negative real
roots for each b.

Now consider the locus of the vertices of the set of parabolas graphed from

Show that the locus is the parabola

Proof:

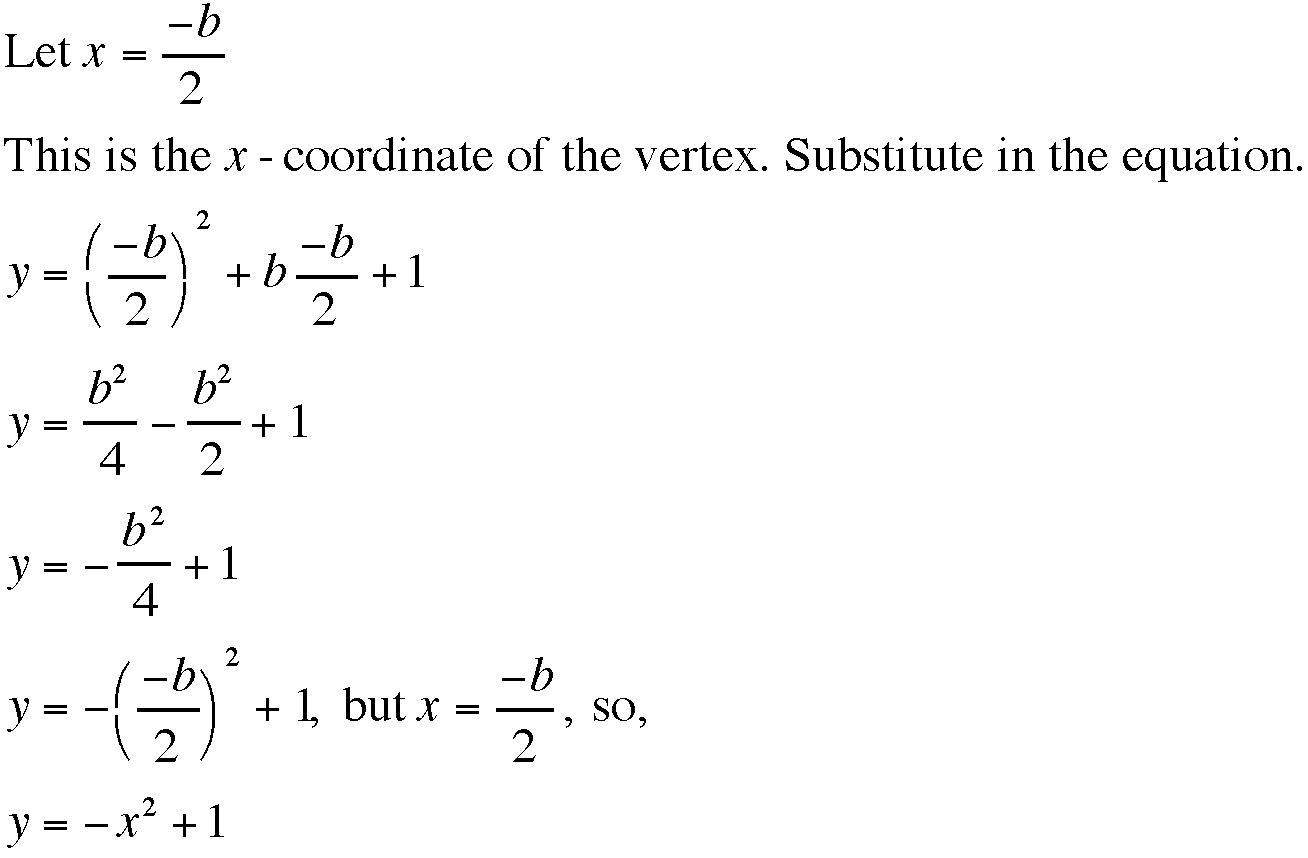
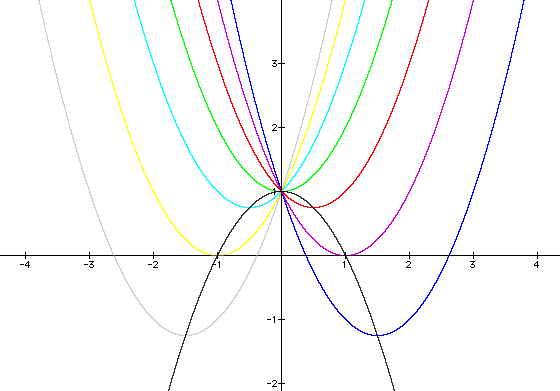
Here is the previous picture with the parabola of the vertices also plotted.

The parabola of the locus of the vertices can be generalized to the equation as follows.

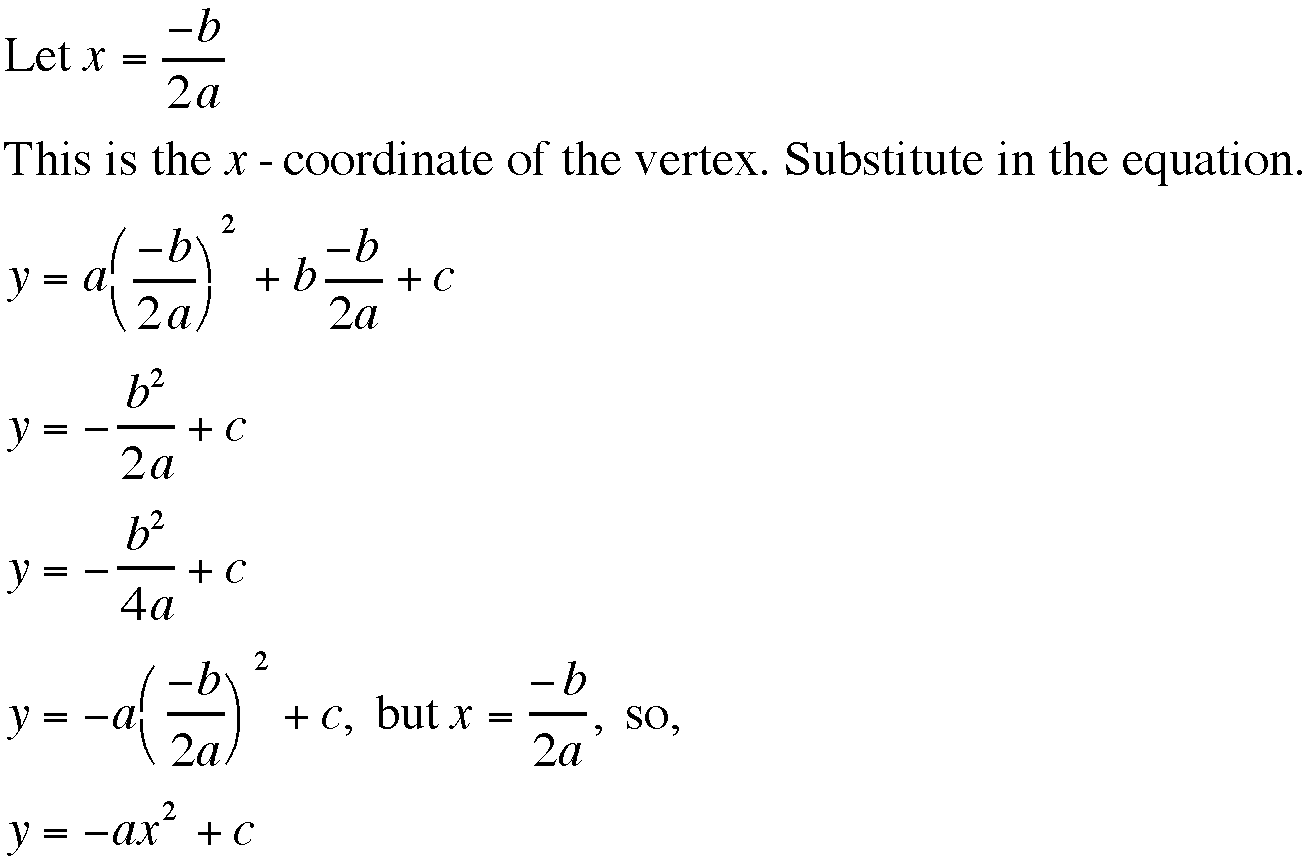
Graphs in the xb plane.

Consider again the equation

Now graph this relation in the xb plane. We get the following graph.

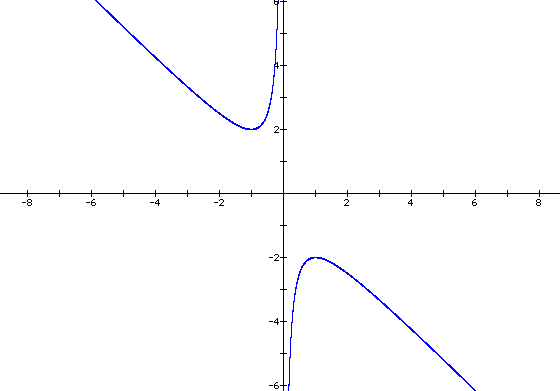
If we take any particular value of b, say b = 4, and overlay this equation on the graph we add a line parallel to the x-axis. If it intersects the
curve in the xb plane the intersection points correspond to the roots of the original equation for that value of b. We have the following graph.

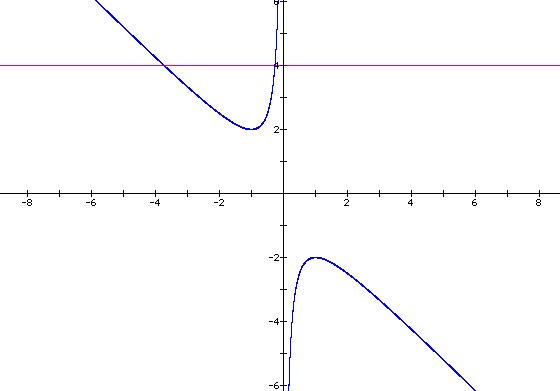
For each value of b we select, we get a horizontal line. It is clear on a single graph that we get two negative real roots of the original equation
when b > 2, one negative real root when b = 2, no real roots for -2 < b < 2, One positive real root when b = -2, and two positive real roots
when b < -2.

Consider the case when c = - 1 rather than + 1.

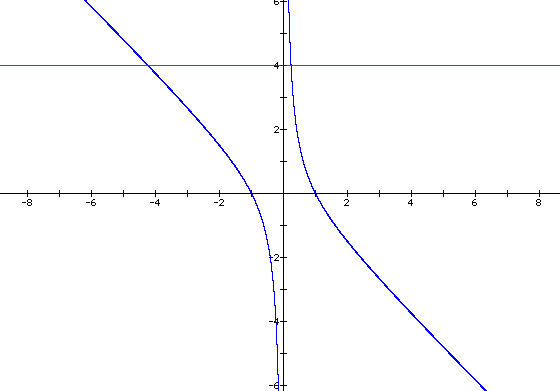
Now it is obvious that there are no complex roots. The roots of the equation are real valued for all real values of b.

Complex Roots

Complex numbers are used extensively in almost every engineering discipline and in the natural sciences. It is unfortunate that complex numbers are associated with the name "imaginary numbers." In engineering and the natural sciences, complex numbers are used to model very real phenomena, such as vibrations in mechanics and reactive power in electrical engineering. Therefore it should be of some interest how the complex roots of a quadratic equation behave with respect to the value of b.

Let's analyze the behavior of the complex roots of with respect to the value of b when -2 < b < 2. The major problem we are going to have here is visualizing the complex roots graphically.

This is an attempt to visualize the complex roots. This graph was created using Graphing Calculator 2.2 and the following equations.

The real part of the complex roots is modelled by the equation:

Notice that this is the first term in the RHS of the quadratic formula.

The imaginary part of the complex roots had to be modelled using two equations, one for the positive complex part and one for the imaginary part of the conjugate. The two equations are:

Notice that the imaginary parts are graphed on the y - axis. So I am using the xy - plane as the complex plane with the y - axis as the imaginary axis, and the xz - plane as the xb - plane. The points of interest, that is, the complex roots, are at the intersection of the plane

with the cylinder in three-space. Lets look at another view of the graph.

Now the z - axis is almost horizontal, the x - axis is coming out of the page and the y - axis is nearly vertical. This gives an almost end-on view of the cylinder. In this perspective, the behavior of the imaginary part of the complex roots is more apparent. As z, that is, b, approaches +- 2, the imaginary part of the roots approaches zero as expected. As z approaches zero, the imaginary part of the complex roots approaches +-i as expected.

Let's rotate the graph again to where we can observe the behavior of the real part of the complex roots.

In this visualization, the x - axis is almost horizontal with positive to the right and the z - axis is almost vertical with positive upward. As expected the graph of the real part of the complex roots is a line with slope of -1/2 going through the origin in the xz - plane.

How are the real and complex roots related as a function of b? We made an attempt to show this using Graphing Calculator 2.2 and the result is shown below.

The domain of the graph is -6 < z < 6. The intersection of the green surfaces and the represent the real roots xz - plane represent the real roots of the equation as b is varied. Unfortunately, the xz - plane is not shown and the intersection would not be viewable if it were shown because of the limitaions of Graphing Calculator 2.2. (There is no way to "see through" a surface to view a surface behind it.) However, we get the idea of what the intersection looks like from the intersection of the green surfaces with the red surfaces.

If we turn the graph so that the x - axis is oblique to the page, we see how the complex roots compare.

The green surface is the equation in three-space. This is the same as the equation that we used to graph the equation in the xb - plane.

The only problem with this method of exploring the complex roots is the limitation of Graphing Calculator 2.2. With some other software packages, such as Mathematica or Matlab, we might have been able to show the intersections of the surfaces we are interested in without actually showing the surfaces. However, these other programs are very expensive when compared to Graphing Calculator 2.2 and may not be affordable to some individuals or schools. Also, Mathematica and Matlab are much more complicated to use than Graphing Calculator 2.2, which can be learned and used successfully by almost any mathematics student in one short lesson. For these reasons, Graphing Calculator is a more useful software package for the average mathematics student.

Conclusion

We have limited our investigation to the behavior of the roots of the equation with respect to the values of the coefficient b. There are many more investigations that can be done varying the other two coefficients. To view a page that contains some of these investigations, click here. We hope that you have a little more appreciation for the behavior and importance of the complex roots of this equation. Other possible explorations include the higher order polynomial equations. These may have more than one pair of complex roots. (But not unless the degree of the polynomial is 4 or higher. Why?) We hope that you will explore some of these as a result of this paper.

RETURN